题目内容
【题目】![]() 在平面直角坐标系中,将点
在平面直角坐标系中,将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() .直接写出点
.直接写出点![]() ,
,![]() 的坐标;23.
的坐标;23.
![]() 在平面直角坐标系中,将第二象限内的点
在平面直角坐标系中,将第二象限内的点![]() 向右平移
向右平移![]() 个单位到第一象限点
个单位到第一象限点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 在平面直角坐标系中.将点
在平面直角坐标系中.将点![]() 沿水平方向平移
沿水平方向平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
【答案】见解析
【解析】
(1)如图,由于将点A(-3,4)向右平移5个单位到点A1,根据平移规律可以得到A1的坐标,又将点A1绕坐标原点顺时针旋转90°到点A2,根据旋转得到△OMA1≌△OM1A2,由此就可以确定A2的坐标;
(2)可以利用(1)中的规律依次分别得到B1的坐标,B2的坐标;
(3)分两种情况:①当把点P(c,d)沿水平方向右平移n个单位到点P1,此时可以利用(2)的规律求出P1和P2的坐标;②当把点P(c,d)沿水平方向左平移n个单位到点P1,那么P1的横坐标和前面的计算方法恰好相反,用减法,然后将点P1绕坐标原点顺时针旋转90°到点P2的坐标的规律也恰好相反,由此可以直接得到P2的坐标.
![]() 如图,∵将点
如图,∵将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
∵又将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,
,
∴![]() ,
,
∴![]() 的坐标
的坐标![]() .
.
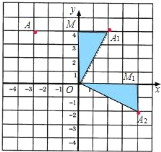
![]() 根据
根据![]() 中的规律得:
中的规律得:
![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() .
.![]() 分两种情况:
分两种情况:
①当把点![]() 沿水平方向右平移
沿水平方向右平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
则![]() 的坐标为
的坐标为![]() ;
;
②当把点![]() 沿水平方向左平移
沿水平方向左平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
然后将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,
,
∴![]() 的坐标
的坐标![]() .
.

练习册系列答案
相关题目