题目内容
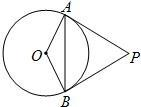 如图,⊙O的半径为2,PA、PB是⊙O的切线,A,B为切点,∠OAB=30度.
如图,⊙O的半径为2,PA、PB是⊙O的切线,A,B为切点,∠OAB=30度.
(1)求∠P的度数;
(2)求△OAB的面积.
解:(1)∵∠OAB=30°,
∴∠AOB=180°-2×30°=120°,
又∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠P=360°-90°-90°-120°=60°.
(2)过点O作OH⊥AB于H,可知AH=BH,
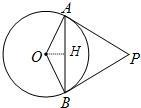
∵∠OAB=30°,OA=2,
∴OH=1,AH= ,
,
∴AB= ,
,
∴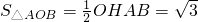 .
.
分析:(1)根据三角形的内角和可求得∠o我度数,再根据四边形的内角和,可求得∠P的度数;
(2)利用勾股定理和三角形的面积公式即可求得△OAB的面积.
点评:本题主要考查了三角形和四边形的内角和,及勾股定理和三角形面积的应用.
∴∠AOB=180°-2×30°=120°,
又∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠P=360°-90°-90°-120°=60°.
(2)过点O作OH⊥AB于H,可知AH=BH,

∵∠OAB=30°,OA=2,
∴OH=1,AH=
 ,
,∴AB=
 ,
,∴
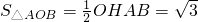 .
.分析:(1)根据三角形的内角和可求得∠o我度数,再根据四边形的内角和,可求得∠P的度数;
(2)利用勾股定理和三角形的面积公式即可求得△OAB的面积.
点评:本题主要考查了三角形和四边形的内角和,及勾股定理和三角形面积的应用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为