题目内容
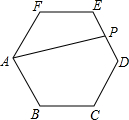
如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
A.2
| B.4 | C.
| D.
|

如图,连接AE,
在正六边形中,∠F=
×(6-2)•180°=120°,
∵AF=EF,
∴∠AEF=∠EAF=
(180°-120°)=30°,
∴∠AEP=120°-30°=90°,
AE=2×2cos30°=2×2×
=2
,
∵点P是ED的中点,
∴EP=
×2=1,
在Rt△AEP中,AP=
=
=
.
故选:C.

在正六边形中,∠F=
| 1 |
| 6 |
∵AF=EF,
∴∠AEF=∠EAF=
| 1 |
| 2 |
∴∠AEP=120°-30°=90°,
AE=2×2cos30°=2×2×
| ||
| 2 |
| 3 |
∵点P是ED的中点,
∴EP=
| 1 |
| 2 |
在Rt△AEP中,AP=
| AE2+EP2 |
(2
|
| 13 |
故选:C.


练习册系列答案
相关题目




