题目内容
如图所示,在平面直角坐标系中,矩形ABCO的两边OA、OC分别在x轴和y轴的正半轴上,OA=4,OC=2。点P从点O出发,沿x轴以每秒1个单位长度的速度向点A匀速运动,当点P到达点A时停止运动。设点P运动的时间是t秒,将线段CP的中点绕点P按顺时针方向旋转90°得到点D,点D随点P的运动而运动,连结DP,DA。
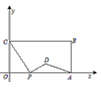
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大?最大面积为多少?
(3)当点P与点O重合时,CO的中点绕点P旋转后的对应点为D1,点P与点A重合时,CA中点绕P点旋转后的对应点为D2,求直线D1D2的解析式;
(4)求出随着点P的运动,点D运动路线的长度。
(2)求t为何值时,△DPA的面积最大?最大面积为多少?
(3)当点P与点O重合时,CO的中点绕点P旋转后的对应点为D1,点P与点A重合时,CA中点绕P点旋转后的对应点为D2,求直线D1D2的解析式;
(4)求出随着点P的运动,点D运动路线的长度。
解:(1)过点D作DE⊥x轴于点E,
则∠DPE=∠COP=90°,
因为∠CPD=90°,
∴∠DPE=90°-∠CPO,
又∵∠OPC=90°-∠CPO,
∴∠DPE=∠OPC,
∴△PED∽△COP,
∴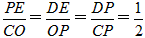 ,
,
∴PE=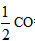 =1,DE=
=1,DE= OE=OP+PE=t+1,
OE=OP+PE=t+1,
∴D点的坐标为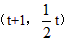 ;
;
(2)PA=4-t,DE= =t,所以S△DPA=
=t,所以S△DPA= =
=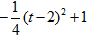 ,
,
∴当t=2时,S△DPA最大,且最大值为1;
(3)D1(1,0),D2(5,2),设直线D1D2的解析式为y=kx+b,所以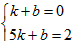 ,解得
,解得 ,
,
∴直线D1D2的解析式为y=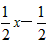 ,
,
(4)将D点坐标代入到解析式中,y=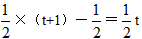 ,
,
∴点D在直线D1D2上,即D点运动的路线是一条线段,起点是D1(1,0),终点是D2(5,2),
D1D2=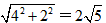 ,∴点D运动路线的长度为
,∴点D运动路线的长度为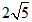 。
。
则∠DPE=∠COP=90°,
因为∠CPD=90°,
∴∠DPE=90°-∠CPO,
又∵∠OPC=90°-∠CPO,
∴∠DPE=∠OPC,
∴△PED∽△COP,
∴
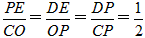 ,
,∴PE=
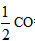 =1,DE=
=1,DE= OE=OP+PE=t+1,
OE=OP+PE=t+1,∴D点的坐标为
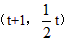 ;
;(2)PA=4-t,DE=
 =t,所以S△DPA=
=t,所以S△DPA= =
=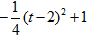 ,
,∴当t=2时,S△DPA最大,且最大值为1;
(3)D1(1,0),D2(5,2),设直线D1D2的解析式为y=kx+b,所以
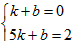 ,解得
,解得 ,
,∴直线D1D2的解析式为y=
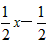 ,
,(4)将D点坐标代入到解析式中,y=
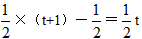 ,
,∴点D在直线D1D2上,即D点运动的路线是一条线段,起点是D1(1,0),终点是D2(5,2),
D1D2=
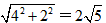 ,∴点D运动路线的长度为
,∴点D运动路线的长度为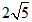 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )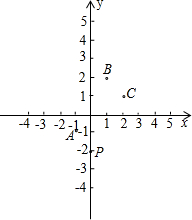 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.