ΧβΡΩΡΎ»ί
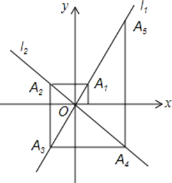
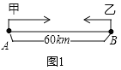
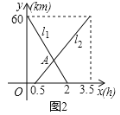
ΓΨΧβΡΩΓΩAΓΔBΝΫΒΊœύΨύ60km,ΦΉ¥”AΒΊ»ΞBΒΊΘ§““¥”BΒΊ»ΞAΒΊΘ§ΆΦ÷–l1ΓΔl2Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥάκBΒΊΒΡΨύάκyΘ®kmΘ©”κΦΉ≥ωΖΔ ±ΦδxΘ®hΘ©ΒΡΚ· ΐΙΊœΒΆΦœσ.
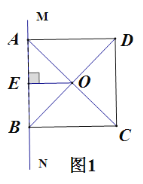
Θ®1Θ©ΗυΨίΆΦœσΘ§÷±Ϋ”–¥≥ω““ΒΡ–– ΜΥΌΕ»ΘΜ
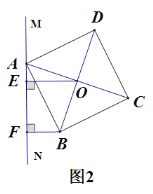
Θ®2Θ©Ϋβ ΆΫΜΒψAΒΡ ΒΦ “β“εΘΜ
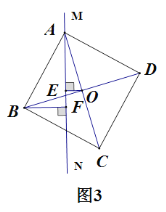
Θ®3Θ©ΦΉ≥ωΖΔΕύ…Ό ±ΦδΘ§ΝΫ»Υ÷°ΦδΒΡΨύάκ«ΓΚΟœύΨύ5kmΘΜ
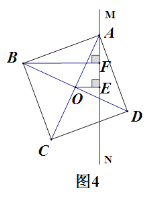
Θ®4Θ©»τ”Οy3Θ®kmΘ©±μ ΨΦΉ““ΝΫ»Υ÷°ΦδΒΡΨύάκΘ§«κ‘ΎΉχ±ξœΒ÷–Μ≠≥ωy3Θ®kmΘ©ΙΊ”Ύ ±ΦδxΘ®hΘ©ΒΡΚ· ΐΙΊœΒΆΦœσΘ§ΉΔΟςΙΊΦϋΒψΒΡ ΐΨί.
ΓΨ¥πΑΗΓΩΘ®1Θ©20km/hΘΜΘ®2Θ©ΒψAΒΡ ΒΦ “β“ε «‘ΎΦΉ≥ωΖΔ1.4–Γ ± ±Θ§ΦΉ““ΝΫ≥Βœύ”ωΘ§¥Υ ±ΨύάκBΒΊ18kmΘΜΘ®3Θ©Β±ΦΉ≥ωΖΔ1.3hΜρ1.5h ±Θ§ΝΫ»Υ÷°ΦδΒΡΨύάκ«ΓΚΟœύΨύ5kmΘΜΘ®4Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©Θ®2Θ©ΗυΨίΚ· ΐΆΦœσ÷–ΒΡ ΐΨίΩ…“‘«σ““ΒΡ–– ΜΥΌΕ»Θ§≤Δ«σ≥ωΒψAΒΡΉχ±ξΘ§ΥΒ≥ωΒψAΒΡ ΒΦ “β“εΘΜ
Θ®3Θ©ΗυΨίΘ®1Θ©÷–ΒΡΚ· ΐΫβΈω ΫΘ§Ω…“‘Ν–≥ωœύ”ΠΒΡΒ» ΫΘ§¥”ΕχΩ…“‘«σΒΟΦΉ≥ωΖΔΕύ…Ό ±ΦδΘ§ΝΫ»Υ÷°ΦδΒΡΨύάκ«ΓΚΟœύΨύ5kmΘΜ
Θ®4Θ©ΗυΨίΚ· ΐΆΦœσ÷–ΒΡ ΐΨίΩ…“‘«σΒΟy3Θ®kmΘ©ΙΊ”Ύ ±ΦδxΘ®hΘ©ΗςΕΈΒΡΚ· ΐΫβΈω ΫΘ§¥”ΕχΩ…“‘Μ≠≥ωœύ”ΠΒΡΆΦœσΘ°
ΫβΘΚΘ®1Θ©”…ΆΦœσΩ…ΒΟΘ§
““ΒΡ–– ΜΥΌΕ»ΈΣΘΚ60Γ¬Θ®3.5-0.5Θ©=20km/h.
Θ®2Θ©…ηl1Ε‘”ΠΒΡΚ· ΐΫβΈω ΫΈΣy1=k1x+b1Θ§ ΒΟ
ΒΟ
Φ¥l1Ε‘”ΠΒΡΚ· ΐΫβΈω ΫΈΣy1=-30x+60Θ§
…ηl2Ε‘”ΠΒΡΚ· ΐΫβΈω ΫΈΣy2=k2x+b2Θ§ Θ§ΒΟ
Θ§ΒΟ
Φ¥l2Ε‘”ΠΒΡΚ· ΐΫβΈω ΫΈΣy2=20x-10Θ§
”÷![]()
Φ¥ΒψAΒΡΉχ±ξΈΣΘ®1.4Θ§18Θ©Θ§
ΓύΒψAΒΡ ΒΦ “β“ε «‘ΎΦΉ≥ωΖΔ1.4–Γ ± ±Θ§ΦΉ““ΝΫ≥Βœύ”ωΘ§¥Υ ±ΨύάκBΒΊ18kmΘΜ
Θ®3Θ©”…Χβ“βΩ…ΒΟΘ§
|Θ®-30x+60Θ©-Θ®20x-10Θ©|=5Θ§
ΫβΒΟΘ§x1=1.3Θ§x2=1.5Θ§
¥πΘΚΒ±ΦΉ≥ωΖΔ1.3hΜρ1.5h ±Θ§ΝΫ»Υ÷°ΦδΒΡΨύάκ«ΓΚΟœύΨύ5kmΘΜ
Θ®4Θ©”…Χβ“βΩ…ΒΟΘ§
Β±0ΓήxΓή0.5 ±Θ§y3=-30x+60Θ§
Β±0.5ΘΦxΓή1.4 ±Θ§y3=y1-y2=Θ®-30x+60Θ©-Θ®20x-10Θ©=-50x+70Θ§
Β±1.4ΘΦxΓή2 ±Θ§y3=y2-y1=Θ®20x-10Θ©-Θ®-30x+60Θ©=50x-70Θ§
Β±2ΘΦxΓή3.5 ±Θ§y3=20x-10Θ§
y3Θ®kmΘ©ΙΊ”Ύ ±ΦδxΘ®hΘ©ΒΡΚ· ΐΙΊœΒΆΦœσ»γΆΦ2Υυ ΨΘ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ