��Ŀ����
����Ŀ��ij��ѧ��ȤС����ȫУ��Χ�������ȡ��50��ͬѧ���С�����ϵij�ɳ������ϲ���ij�ɳС�ԡ��������������ʾ���������Ƴ���ͼ��ʾ�IJ���������ͳ��ͼ��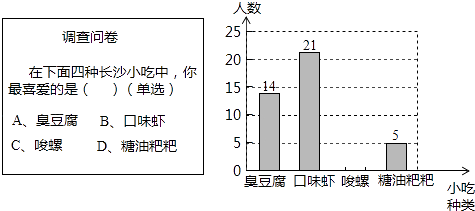
�����������Ϣ����������⣺
��1���벹ȫ����ͳ��ͼ��
��2����ȫУ��2000��ͬѧ�������ȫУͬѧ����ϲ��������������ͬѧ�ж����ˣ�
��3����һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ����С�Ե����A��B��C��D�����������һ��С��Ȼ��Żأ������������һ��С�������б�������ͼ�ķ��������ǡ�����ζ�������A���ĸ��ʣ�
���𰸡�
��1���⣺��������ã�ϲ�������ݡ�����Ϊ��50����14+21+5��=10���ˣ���
��ȫͳ��ͼ����ͼ��ʾ��

��2���⣺��������ã�2000�� ![]() ��100%=560���ˣ���
��100%=560���ˣ���
�����ȫУͬѧ����ϲ��������������ͬѧ��560�ˣ�
��3���⣺�б����£�
A | B | C | D | |
A | ��A��A�� | ��B��A�� | ��C��A�� | ��D��A�� |
B | ��A��B�� | ��B��B�� | ��C��B�� | ��D��B�� |
C | ��A��C�� | ��B��C�� | ��C��C�� | ��D��C�� |
D | ��A��D�� | ��B��D�� | ��C��D�� | ��D��D�� |
���еȿ��ܵ������16�֣�����ǡ�����ζ�������A���������1�֣�
��P= ![]() ��
��
����������1���������������ڸ�����Ƶ��֮�Ϳ����ϲ�������ݡ���������Ȼ���ٲ�ȫ����ͳ��ͼ���ɣ�
��2�����ݰٷֱ�=Ƶ���������������ϲ�������������İٷֱȣ�Ȼ��������Ƶ��=�������ٷֱ���⼴�ɣ�
��3���б��ó����еȿ��ܵ���������ҳ�ǡ�����ζ�������A�������������������ø��ʹ�ʽ��⼴��.
�����㾫����������Ĺؼ�������������ͳ��ͼ�����֪ʶ������������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯������Լ����б�������״ͼ�������⣬�˽һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�

 ������������ϵ�д�
������������ϵ�д�����Ŀ�����ֺͿ�ѧС���ͬѧ�������ϻ�ȡ�������ڿ����д������ٶ�������¶�֮���ϵ��һЩ���ݣ����±���
�¶�/ | -20 | -10 | 0 | 10 | 20 | 30 |
����/�� | 318 | 324 | 330 | 336 | 342 | 348 |
����˵�����������ǣ� ��
A.������仯�����У����¶�Ϊ10![]() ʱ��������336
ʱ��������336![]()
B.�¶�Խ�ߣ�����Խ��
C.�������¶�Ϊ20![]() ʱ������5
ʱ������5![]() ���Դ���1740
���Դ���1740![]()
D.���¶�ÿ����10![]() ����������6
����������6![]()