Question

如图，AD是⊙O的内接△ABC的高，AE是⊙O的直径，求证：AB•AC=AD•AE．

Answer 1

分析：首先连接BE，由AD是⊙O的内接△ABC的高，AE是⊙O的直径，可得∠ABE=∠ADC=90°，又由在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，可得∠E=∠C，即可证得△ABE∽△ADC，然后由相似三角形的对应边成比例，证得AB•AC=AD•AE．

解答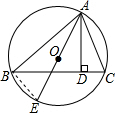：证明：连接BE，
∵AD是⊙O的内接△ABC的高，AE是⊙O的直径，
∴∠ABE=∠ADC=90°，
∵∠E=∠C，
∴△ABE∽△ADC，
∴AB：AD=AE：AC，
∴AB•AC=AD•AE．

点评：此题考查了相似三角形的判定与性质以及圆周角定理．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．