题目内容
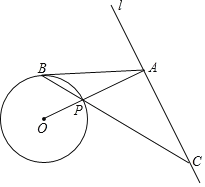
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,若⊙
,若⊙![]() 的圆心在线段
的圆心在线段![]() 上,且⊙
上,且⊙![]() 与
与![]() 都相切,则⊙
都相切,则⊙![]() 的半径是___________.
的半径是___________.

【答案】![]()
【解析】
过O点作OM⊥AC、ON⊥AB,设⊙O半径为R,求出OM=MP=R,根据勾股定理求出BP,OP,求出BO,根据切线长定理求出AN=AM=1+R,求出BN,在Rt△BNO中,根据勾股定理求出即可.
过O点作OM⊥AC、ON⊥AB,
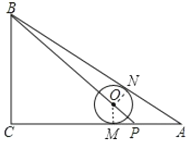
∵⊙O与AB、AC都相切,
∴AN=AM,OM⊥CP,ON⊥AB,
∴∠BNO=∠OMP=90 ![]() ,
,
设⊙O半径为R,
在Rt△ABC中,∠C=90 ![]() ,AC=4,AB=5,由勾股定理得:BC=3,
,AC=4,AB=5,由勾股定理得:BC=3,
∵AP=1,AC=4,
∴CP=41=3=BC,
∴∠CBP=∠CPB=45 ![]() ,
,
∵∠OMP=90 ![]() ,
,
∴∠MOP=45 ![]() =∠OPM,
=∠OPM,
∴OM=MP=R,
在Rt△OMP中,由勾股定理得:PO=![]() R,
R,
在Rt△BCP中,由勾股定理得:BP=3 ![]() ,
,
则BO=3![]()
![]() R,AM=AN=1+R,
R,AM=AN=1+R,
∴BN=BAAN=5(1+R)=4R,
∵在Rt△BNO中,由勾股定理得:BN2+ON2=BO2,
∴(4R)2+R2=(3![]()
![]() R)2,
R)2,
解得:R=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目