题目内容
 如图,AO⊥BO,CO⊥DO,∠AOD与∠BOC的度数之比是4:5,则∠AOD的度数是
如图,AO⊥BO,CO⊥DO,∠AOD与∠BOC的度数之比是4:5,则∠AOD的度数是
- A.20°
- B.30°
- C.80°
- D.100°
C
分析:根据垂线的性质由AO⊥BO,CO⊥DO得到∠AOB=90°,∠DOC=90°,设∠AOD=4x,则∠BOC=5x,根据周角的定义得到∠AOB+∠DOC+∠AOD+∠BOC=360°,即90°+90°+4x+5x=360°,可解得x=20°,则∠AOD=4x=80°.
解答:∵AO⊥BO,CO⊥DO,
∴∠AOB=90°,∠DOC=90°,
设∠AOD=4x,则∠BOC=5x,
∵∠AOB+∠DOC+∠AOD+∠BOC=360°,
∴90°+90°+4x+5x=360°,
∴x=20°,
∴∠AOD=4x=80°.
故选C.
点评:本题考查了垂线的性质:当两条直线垂直时,那么这两条直线相交所形成的角为90°.也考查了周角的定义.
分析:根据垂线的性质由AO⊥BO,CO⊥DO得到∠AOB=90°,∠DOC=90°,设∠AOD=4x,则∠BOC=5x,根据周角的定义得到∠AOB+∠DOC+∠AOD+∠BOC=360°,即90°+90°+4x+5x=360°,可解得x=20°,则∠AOD=4x=80°.
解答:∵AO⊥BO,CO⊥DO,
∴∠AOB=90°,∠DOC=90°,
设∠AOD=4x,则∠BOC=5x,
∵∠AOB+∠DOC+∠AOD+∠BOC=360°,
∴90°+90°+4x+5x=360°,
∴x=20°,
∴∠AOD=4x=80°.
故选C.
点评:本题考查了垂线的性质:当两条直线垂直时,那么这两条直线相交所形成的角为90°.也考查了周角的定义.

练习册系列答案
相关题目
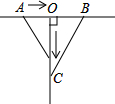 如图,AO=BO=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由点A以2cm/s的速度向点B爬行,同时另一只蚂蚁由点O以3cm/s的速度沿OC方向爬行,则
如图,AO=BO=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由点A以2cm/s的速度向点B爬行,同时另一只蚂蚁由点O以3cm/s的速度沿OC方向爬行,则 如图,AO⊥BO,直线CD经过点O,∠AOC=110°,则∠BOD=
如图,AO⊥BO,直线CD经过点O,∠AOC=110°,则∠BOD=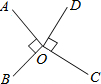 如图,AO⊥BO,CO⊥DO,∠AOD与∠BOC的度数之比是4:5,则∠AOD的度数是( )
如图,AO⊥BO,CO⊥DO,∠AOD与∠BOC的度数之比是4:5,则∠AOD的度数是( ) 已知:如图,AO⊥BO,∠1=∠3.求证:CO⊥DO.
已知:如图,AO⊥BO,∠1=∠3.求证:CO⊥DO.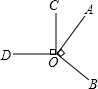 如图,AO⊥BO,OC⊥OD,∠BOD=3∠AOC.则∠BOD=
如图,AO⊥BO,OC⊥OD,∠BOD=3∠AOC.则∠BOD=