题目内容
13.先化简,再求值:(1+$\frac{2}{m-1}$)÷$\frac{m+1}{{m}^{2}-2m+1}$,其中m=tan45°+2cos30°.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,利用特殊角的三角函数值求出m的值,代入计算即可求出值.
解答 解:原式=$\frac{m-1+2}{m-1}$•$\frac{(m-1)^{2}}{m+1}$=$\frac{m+1}{m-1}$•$\frac{(m-1)^{2}}{m+1}$=m-1,
当m=tan45°+2cos30°=1+$\sqrt{3}$时,原式=$\sqrt{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
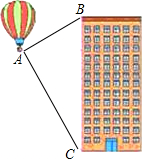 如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米.
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米. 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.
如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.
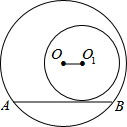 如图,⊙O1内含于⊙O,⊙O的弦AB切⊙O1于点C,OO1∥AB,若⊙O的半径为5cm,⊙O1的半径为3cm,则AB的长为8cm.
如图,⊙O1内含于⊙O,⊙O的弦AB切⊙O1于点C,OO1∥AB,若⊙O的半径为5cm,⊙O1的半径为3cm,则AB的长为8cm.