题目内容
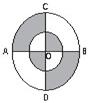
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3,求AG,MN的长.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3,求AG,MN的长.

(1)在Rt△ABE和Rt△AGE中, ,
, ,
,
∴△ABE≌△AGE. ∴ .
.
同理, .
.
∴ .
.
(2) .
.
∵ ,
, ,
,
∴ . ∴
. ∴ .
.
又∵ ,
, ,
,
∴△AMN≌△AHN. ∴ .
.
∵ ,
, ,
,
∴ . ∴
. ∴ .
.
∴ . ∴
. ∴ .
.
(3)由(1)知, ,
, .
.
设 ,则
,则 ,
, .
.
∵ ,
,
∴ .
.
解这个方程,得 ,
, (舍去负根).
(舍去负根).
∴ .
.
∴ .
.
在(2)中, ,
, ,
,
∴ .
.
设 ,则
,则 .
.
∴ .即
.即 .
.

 ,
, ,
,∴△ABE≌△AGE. ∴
 .
.同理,
 .
.∴
 .
.(2)
 .
.∵
 ,
, ,
,∴
 . ∴
. ∴ .
.又∵
 ,
, ,
,∴△AMN≌△AHN. ∴
 .
.∵
 ,
, ,
,∴
 . ∴
. ∴ .
.∴
 . ∴
. ∴ .
.(3)由(1)知,
 ,
, .
.设
 ,则
,则 ,
, .
.∵
 ,
,∴
 .
.解这个方程,得
 ,
, (舍去负根).
(舍去负根).∴
 .
.∴
 .
.在(2)中,
 ,
, ,
,∴
 .
.设
 ,则
,则 .
.∴
 .即
.即 .
.
(1)根据高AG与正方形的边长相等,证明三角形相等,进而证明角相等,从而求出解.
(2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
(3)设出线段的长,结合方程思想,用数形结合得到结果.
(2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
(3)设出线段的长,结合方程思想,用数形结合得到结果.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目



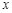 轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转
轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转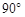 ,得到线段AB.过点B作
,得到线段AB.过点B作 轴的垂线,交直线BE于点D.运动时间为
轴的垂线,交直线BE于点D.运动时间为 秒.
秒.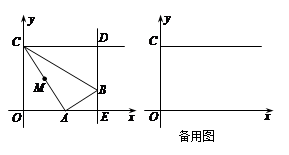
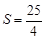 ?
?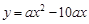 的顶点在△ABM内部(不包括边),求a的取值范围.
的顶点在△ABM内部(不包括边),求a的取值范围. 、
、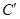 。
。 ;
;
 可以由△ABC绕点 A顺
可以由△ABC绕点 A顺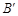 与点B是对应点,点
与点B是对应点,点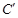 与点C是对应点),连接
与点C是对应点),连接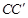 ,则∠
,则∠
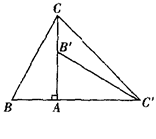
 内部一点,且
内部一点,且 ,求
,求 的度数.
的度数.

 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△ ,连结
,连结 . 则△
. 则△ 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形 中.
中. .
. 中,
中, ,点
,点 在
在 上,且
上,且 ,
, ,若将
,若将 绕点
绕点 顺时针旋转得到Rt
顺时针旋转得到Rt ,且
,且 落在
落在 的延长线上,联结
的延长线上,联结 交
交 ,则
,则 = .
= . 