题目内容
若⊙O的半径长是4cm，圆外一点A与⊙O上各点的最远距离是12cm，则自A点所引⊙O的切线长为
- A.16cm
- B.
- C.
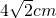
- D.
B
分析：圆外一点A与⊙O上各点的最远距离是12cm，即AC=12cm，求得AB的长，然后利用切割线定理即可求得切线长AD的长．
解答：
解：根据题意得：AC=12cm，则AB=12-4-4=4cm．
∵AD是圆的切线，
∴AD2=AB•AC=4×12=48．
∴AD=4
cm．
故选B．
点评：本题考查了切割线定理，理解圆外一点A与⊙O上各点的最远距离是12cm，即AC=12cm是关键．
分析：圆外一点A与⊙O上各点的最远距离是12cm，即AC=12cm，求得AB的长，然后利用切割线定理即可求得切线长AD的长．
解答：
解：根据题意得：AC=12cm，则AB=12-4-4=4cm．∵AD是圆的切线，
∴AD2=AB•AC=4×12=48．
∴AD=4
cm．故选B．
点评：本题考查了切割线定理，理解圆外一点A与⊙O上各点的最远距离是12cm，即AC=12cm是关键．
练习册系列答案
相关题目
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为6，sinB=| 1 |
| 3 |
| A、3 | B、4 | C、5 | D、6 |
若一个扇形的面积是12π，它的弧长是4π，则它的半径是（ ）
| A、3 | B、4 | C、5 | D、6 |
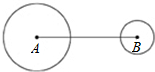如图，圆A、圆B的半径分别为4、2，且AB=12．若作一圆C使得三圆的圆心在同一直在线，且圆C与圆A外切，圆C与圆B相交于两点，则下列何者可能是圆C的半径长（ ）
如图，在⊙O中，AB为弦，OC⊥AB于点E，若⊙O的半径为5，CE=2，则AB的长是（ ）
，则线段AC的长是（ ）