题目内容
如图，在⊙O中，AB为弦，OC⊥AB于点E，若⊙O的半径为5，CE=2，则AB的长是（ ）分析：首先连接OA，由⊙O的半径为5，CE=2，可得OA=5，OC=3，然后由勾股定理求得AE的长，由垂径定理即可求得AB的长．
解答：
解：连接OA，
∵OC⊥AB，
∴AE=
AB，
∵⊙O的半径为5，CE=2，
∴OA=5，OE=5-2=3，
在Rt△AOE中，AE=
=4，
∴AB=2AE=8．
故选D．
解：连接OA，∵OC⊥AB，
∴AE=
| 1 |
| 2 |
∵⊙O的半径为5，CE=2，
∴OA=5，OE=5-2=3，
在Rt△AOE中，AE=
| OA2-OC2 |
∴AB=2AE=8．
故选D．
点评：此题考查了垂径定理以及勾股定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
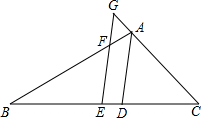如图，在△ABC中，AB＞AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．
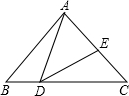如图，在△ABC中，AB=AC，D为BC边上一点，且∠BAD=30°，若AD=DE，∠EDC=33°，则∠DAE的度数为
如图，在△ABC中，AB=AC，D是△ABC内一点，且BD=DC．求证：∠ABD=∠ACD．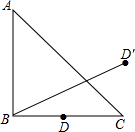
如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
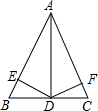如图，在△ABC中，AB=AC，D点是BC的中点，DE⊥AB于E点，DF⊥AC于F点，则图中全等三角形共有