题目内容
 如图,已知:在△ABC中,∠A=∠B,CE是外角∠ACD的平分线、请问:CE与AB是否平行?
如图,已知:在△ABC中,∠A=∠B,CE是外角∠ACD的平分线、请问:CE与AB是否平行?试说明理由.
答:
理由如下:
∵∠A=∠B,∠ACD是△ABC的外角,
∴∠ACD=∠
∵CE是外角∠ACD的平分线,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE∥AB(
分析:要证明CE与AB平行,则要通过证明角与角之间的等量关系证明.
解答:解:CE∥AB.
理由如下:
∵∠A=∠B,∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=2∠A,
∵CE是外角∠ACD的平分线,
∴∠ACE=
∠ACD=
×2∠A=∠A,
∴CE∥AB(内错角相等,两直线平行)
理由如下:
∵∠A=∠B,∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=2∠A,
∵CE是外角∠ACD的平分线,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE∥AB(内错角相等,两直线平行)
点评:本题主要考查平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.

练习册系列答案
相关题目
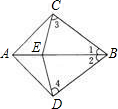
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.

