题目内容
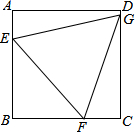 如图,正方形ABCD中,点E、F、G分别为AB、BC、CD边上的点,EB=3cm,GC=4cm,连接EF、FG、GE恰好构成一个等边三角形,则正方形的边长为
如图,正方形ABCD中,点E、F、G分别为AB、BC、CD边上的点,EB=3cm,GC=4cm,连接EF、FG、GE恰好构成一个等边三角形,则正方形的边长为考点:正方形的性质,等边三角形的性质,勾股定理
专题:
分析:过G作GM⊥AB于M,设BF=x,CF=y,利用勾股定理得出在Rt△GEM中,EG2=1+(x+y)2,在Rt△GCFM中,GF2=16+y2在Rt△EBF中,EF2=9+x2;进一步联立得出方程,求得方程的解即可解决问题.
解答:解:如图,
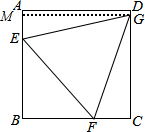
过G作GM⊥AB于M,设BF=x,CF=y,
则ME=CG-BE=1,
在Rt△GEM中,EG2=1+(x+y)2,
在Rt△GCFM中,GF2=16+y2
在Rt△EBF中,EF2=9+x2
∵等边△EFG中EF=EG=GF,
∴9+x2=16+y2,即x2-y2=7 (1)
1+(x+y)2=9+x2,即y2+2xy=8 (2)
(1)×8-(2)×7后整理得,8x2-14xy-15y2=0,
两边同除以y2得8(
)2+14(
)-15=0,
设a=
,则有8a2-14a-15=0
(2a-5)(4a+3)=0,解之得a=
或a=-
(舍去)
所以x=
y,代入(1)得,
y2=7,
y=
cm.
所以x=
y=
,
所以正方形边长=x+y=
cm.
故答案为:
.

过G作GM⊥AB于M,设BF=x,CF=y,
则ME=CG-BE=1,
在Rt△GEM中,EG2=1+(x+y)2,
在Rt△GCFM中,GF2=16+y2
在Rt△EBF中,EF2=9+x2
∵等边△EFG中EF=EG=GF,
∴9+x2=16+y2,即x2-y2=7 (1)
1+(x+y)2=9+x2,即y2+2xy=8 (2)
(1)×8-(2)×7后整理得,8x2-14xy-15y2=0,
两边同除以y2得8(
| x |
| y |
| x |
| y |
设a=
| x |
| y |
(2a-5)(4a+3)=0,解之得a=
| 5 |
| 2 |
| 3 |
| 4 |
所以x=
| 5 |
| 2 |
| 21 |
| 4 |
y=
2
| ||
| 3 |
所以x=
| 5 |
| 2 |
5
| ||
| 3 |
所以正方形边长=x+y=
7
| ||
| 3 |
故答案为:
7
| ||
| 3 |
点评:此题考查正方形的性质,勾股定理,以及利用方程的思想解决有关图形的计算问题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

 如图,AB∥CD,OF平分∠AOE,∠1=40°,则∠2是多少度?
如图,AB∥CD,OF平分∠AOE,∠1=40°,则∠2是多少度? 如图,在直角坐标系中,如果△AOB≌△COD,并且A,D两点的坐标分别为A(0,3)和D(0,-2),那么B点坐标
如图,在直角坐标系中,如果△AOB≌△COD,并且A,D两点的坐标分别为A(0,3)和D(0,-2),那么B点坐标 小涛在家打扫卫生,一不小心把一块三角形的玻璃台板打碎了,如图,如果要配一块完全一样的玻璃,至少要带
小涛在家打扫卫生,一不小心把一块三角形的玻璃台板打碎了,如图,如果要配一块完全一样的玻璃,至少要带 已知:如图,AD∥BC,BD平分∠ABC,∠A=46°,则∠ADB=
已知:如图,AD∥BC,BD平分∠ABC,∠A=46°,则∠ADB=