题目内容
(2013•黄石)解方程组:
.
|
分析:先由第二个方程得:x=
③,再把③代入①得:2×(
)2-y2=
,求出y1、y2,再代入③即可.
3+2
| ||
| 2 |
3+2
| ||
| 2 |
| 1 |
| 2 |
解答:解:
,
由②得:x=
③,
把③代入①得:2×(
)2-y2=-
,
化简得:9y2+6
y+5=0,
即:(3y+
)2=0
解得:y1=y2=-
,
代入③得:x1=x2=-
,
∴原方程组的解为
.
|
由②得:x=
3+2
| ||
| 2 |
把③代入①得:2×(
3+2
| ||
| 2 |
| 1 |
| 2 |
化简得:9y2+6
| 5 |
即:(3y+
| 5 |
解得:y1=y2=-
| ||
| 3 |
代入③得:x1=x2=-
| 1 |
| 6 |
∴原方程组的解为
|
点评:此题考查了高次方程,关键是利用代入法把高次方程转化成低次方程,注意结果有两种情况.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
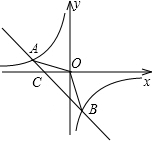 (2013•黄石模拟)如图,已知A(-4,n),B(1,-4)是一次函数y=kx+b的图象和反比例函数
(2013•黄石模拟)如图,已知A(-4,n),B(1,-4)是一次函数y=kx+b的图象和反比例函数