Question

已知：等边中，点O是边AC,BC的垂直平分线的交点，M,N分别在直线AC, BC上，且．

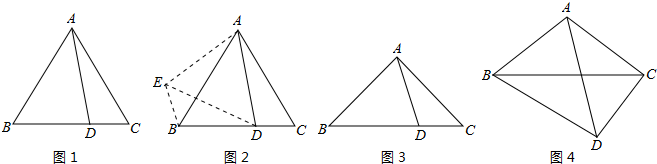
1. 如图1，当CM=CN时， M、N分别在边AC、BC上时，请写出AM、CN 、MN三者之间的数量关系；

2.  如图2，当CM≠CN时，M、N分别在边AC、BC上时，（1）中的结论是否仍然成立？若成立，请你加以证明；若不成立，请说明理由；

3.   如图3，当点M在边AC上，点N在BC 的延长线上时，请直接写出线段AM、CN 、MN三者之间的数量关系．

 

Answer 1

【答案】

 

1.

2.

   证明：过点O 作易得

             

    在边AC上截得DN’=NE,连结ON’,

        ∵ DN’=NE,

           OD=OE,

           ∠ODN’=∠OEN

       

        ∴ON’=OE.  ∠DON’=∠NOE.

         

          ∴∠MOD+∠NOE=60⁰.

         ∴∠MOD+∠DON’=60⁰.

        易证.

         ∴MN’=MN.

3.

【解析】

1.由CM=CN得出△CMN是等边三角形，它与△ABC的相似比是1：3，从而得出；

2.过点O 作在边AC上截得DN’=NE,连结ON’，先证出得出ON’=OE.  ∠DON’=∠NOE.易证出，利用等量代换得出；

3.方程同上。