Question

如图，AB＝CD，点E、F分别是BC、AD中点，延长BA，CD分别与EF的延长线交于点P、Q，则BP与CQ的大小关系是BP      CQ（填“＞”“＜”“＝”） 。

 

Answer 1

【答案】

=

【解析】

试题分析：连接BD，取BD的中点M，连接EM、FM，延长QE到点O，使QE=OE，则可证得△BOE≌△COQ，所以BO=CQ，∠O=∠CQF，根据三角形的中位线性质可得FM//AB且FM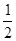＝AB，EM//CD且EM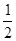＝CD，再结合AB＝CD可得EM＝FM，即可证得∠MEF＝∠MFE，再根据平行线的性质可得∠BPF＝∠CQF，问题得证.

连接BD，取BD的中点M，连接EM、FM，延长QE到点O，使QE=OE，

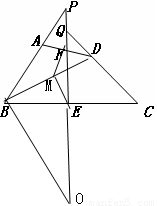
则可证得△BOE≌△COQ

所以BO＝CQ，∠O＝∠CQF

因为F是AD的中点

所以FM是△ABD的中位线

所以FM//AB且FM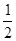＝AB

同理EM//CD且EM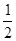＝CD

因为AB＝CD

所以EM＝FM

所以∠MEF＝∠MFE

因为∠BPF＝∠MFE，∠CQF＝∠MEF

所以∠BPF＝∠CQF

因为∠O＝∠CQF

所以∠BPF＝∠O

所以BP＝BO

因为BO＝CQ

所以BP＝CQ.

考点：三角形的中位线定理，平行线的性质

点评：解题的关键是熟记三角形的中位线定理：三角形的中位线平行于第三边，且等于第三边的一半.