Question

已知直线y=kx+b（k≠0），其中k、b可取正数或负数，试求直线y=kx+b经过第二、三、四象限的概率（用树状图或列表法求解）

Answer 1

分析：列举出所有情况，看k，b都是负数的情况占所有情况的多少即可．

解答：解：

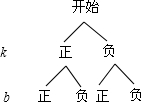
共有4种情况，k，b都是负数的情况只有1种，
∴直线y=k x+b经过第二、三、四象限的概率P=

1

4

（即k＜0，b＜0）．

点评：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=

m

n

；一次函数经过二、三、四象限，比例系数和常数项均为负数．