题目内容
在直角坐标平面中,已知点P(a,b)(|a|≠|b|),设点P关于直线y=x的对称点为Q,点P关于原点的对称点为R,则△PQR的形状是
- A.锐角三角形
- B.直角三角形
- C.钝角三角形
- D.不能确定
B
分析:根据平面内两点关于关于原点对称的点,横坐标与纵坐标都互为相反数,得出R点,再根据平面内点关于y=x对称的点的特点,得出Q点,根据点的特点推理出OQ=OP=OR,再根据直角三角形性质得出结论.
解答: 解:如图,
解:如图,
∵点P关于直线y=x对称
∴确定点Q,
∵点P关于原点对称,
∴确定点R,
根据平面内点关于y=x对称的点的特点,
∴OQ=OP,
又∵P,Q点关于原点对称,
∴OP=OR,
∴OQ=OP=OR,
即:OQ= PR,
PR,
∴△PQR斜边上的中线等于斜边的一半,
∴△PQR为直角三角形,
故选B.
点评:本题主要考查了根据平面内两点关于关于原点对称的点的特点,平面内点关于y=x对称的点的特点,同时考查了直角三角形斜边上的中线等于斜边的一半的特点,该题比较综合.
分析:根据平面内两点关于关于原点对称的点,横坐标与纵坐标都互为相反数,得出R点,再根据平面内点关于y=x对称的点的特点,得出Q点,根据点的特点推理出OQ=OP=OR,再根据直角三角形性质得出结论.
解答:
 解:如图,
解:如图,∵点P关于直线y=x对称
∴确定点Q,
∵点P关于原点对称,
∴确定点R,
根据平面内点关于y=x对称的点的特点,
∴OQ=OP,
又∵P,Q点关于原点对称,
∴OP=OR,
∴OQ=OP=OR,
即:OQ=
 PR,
PR,∴△PQR斜边上的中线等于斜边的一半,
∴△PQR为直角三角形,
故选B.
点评:本题主要考查了根据平面内两点关于关于原点对称的点的特点,平面内点关于y=x对称的点的特点,同时考查了直角三角形斜边上的中线等于斜边的一半的特点,该题比较综合.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
在直角坐标平面中,已知点P(a,b)(|a|≠|b|),设点P关于直线y=x的对称点为Q,点P关于原点的对称点为R,则△PQR的形状是( )
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、不能确定 |
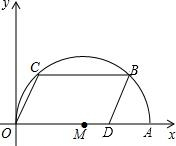 (2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
(2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.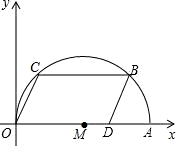 在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.