Question

在玉溪州大河旁边的路灯杆顶上有一个物体，它的抽象几何图形如图，若AB=4，AC=10，∠ABC=60°，求B、C两点间的距离．

Answer 1

解：如图．
过A点作AD⊥BC于点D．
在Rt△ABD中，
∵∠ABC=60°，
∴∠BAD=30°．
∵AB=4，
∴BD=2．
∴AD=2．
在Rt△ADC中，AC=10，
∴CD=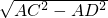==2．
∴BC=2+2．
答：B、C两点间的距离为2+2．
分析：作AD⊥BC于点D，先根据三角函数的定义求出AD，再根据勾股定理求出CD的长．
点评：解答此题的关键是灵活运用解直角三角形的知识，把实际问题转化为数学问题加以解决．