Question

【题目】若一个矩形的短边与长边的比值为（黄金分割数），我们把这样的矩形叫做黄金矩形．

操作：请你在如图所示的黄金矩形中，以短边为一边作正方形；

探究：在中的四边形是不是黄金矩形？若是，请予以证明；若不是，请说明理由．

Answer 1

【答案】（1）画图见解析；（2）四边形是黄金矩形，证明见解析．

【解析】

（1）只需在矩形的长上截取AE=AD，DF=AD，连接EF即可；

（2）可以结合（1）中正方形的性质求得矩形EBCF的宽与长的比进行分析．

（1）如图：

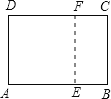
以A为圆心，在AB上截取AE=AD，以D为圆心，在DC上截取DF=DA，连接EF，所以四边形AEFD为所求作的正方形；

（2）四边形是黄金矩形．

证明：∵四边形是正方形，

∴，

∴，

∵四边形是矩形，

∴

∴，

∴四边形是矩形．

设，，则有，

∴，

∴矩形是黄金矩形．