题目内容
3.根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.(1)AB=10cm,BC=12cm,AC=15cm,A′B′=150cm,B′C′=180cm,A′C′=225cm.
(2)∠A=70°,∠B=48°,∠A′=70°,∠C′=62°.
分析 (1)通过计算得出两个三角形三边成比例,即可得出结论;
(2)由三角形内角和定理求出∠C,得出∠A=∠A′,∠C=∠C′,即可得出结论.
解答 解:(1)△ABC∽△A′B′C′,理由如下:
∵$\frac{AB}{A′B′}=\frac{10}{150}=\frac{1}{15}$,$\frac{BC}{B′C′}=\frac{12}{180}=\frac{1}{15}$,$\frac{AC}{A′C′}=\frac{15}{225}=\frac{1}{15}$,
∴$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′;
(2)△ABC∽△A′B′C′,理由如下:
∵∠A=70°,∠B=48°,
∴∠C=180°-∠A-∠B=62°,
∵∠A′=70°,∠C′=62°,
∴∠A=∠A′,∠C=∠C′,
∴△ABC∽△A′B′C′.
点评 本题考查相似三角形的判定、三角形内角和定理;熟练掌握相似三角形的判定方法,通过计算得出三边成比例或两角对应相等是解决问题的关键.

练习册系列答案
相关题目
13.若a+b=-1,则3a2+3b2+6ab+3的值是( )
| A. | 0 | B. | -3 | C. | 6 | D. | 3 |
13.某校举行元旦文娱演出,由参加演出的10个班各推选一名评委,每个节目演出后的得分取各评委给分的平均数,下面是对某班的一个节目各评委给出的评分表:
(1)你对5号和9号评委给出的分有何想法?
(2)10位评委的平均得分是多少?此得分能否反映该节目的水平?
(3)如果去掉一个最高分和去掉一个最低分,再计算平均数应是多少?后一平均数能反映出该节目实际水平吗?
(4)一般情形,如果评委较多,为了使评分能反映实际水平,还可做怎样的改进?
| 评委号数 | 评分 | 评委号数 | 评分 |
| 1 | 7.20 | 6 | 7.30 |
| 2 | 7.25 | 7 | 7.20 |
| 3 | 7.00 | 8 | 7.10 |
| 4 | 7.10 | 9 | 6.20 |
| 5 | 10.00 | 10 | 7.15 |
(2)10位评委的平均得分是多少?此得分能否反映该节目的水平?
(3)如果去掉一个最高分和去掉一个最低分,再计算平均数应是多少?后一平均数能反映出该节目实际水平吗?
(4)一般情形,如果评委较多,为了使评分能反映实际水平,还可做怎样的改进?
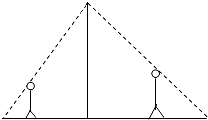 如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米?
如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米?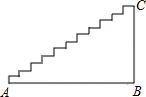 某宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红地毯,如果主楼梯的坡度为1:$\sqrt{3}$,且楼梯的竖直高度为3m.至少需要多长的地毯?(精确到0.1m)
某宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红地毯,如果主楼梯的坡度为1:$\sqrt{3}$,且楼梯的竖直高度为3m.至少需要多长的地毯?(精确到0.1m)