题目内容
按要求完成各题(1)解下列分式方程
①
| 2 |
| x |
| 3 |
| x+1 |
②
| 2-x |
| x-3 |
| 1 |
| 3-x |
(2)先化简,后求值
①
| x2-4x |
| x2-8x+16 |
②(
| a |
| a-b |
| a2 |
| a2-2ab+b2 |
| a |
| a+b |
| a2 |
| a2-b2 |
分析:(1)①的最简公分母是x(x+1),方程两边都乘最简公分母,可把分式方程转换为整式方程求解;
②观察可得最简公分母是(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)①先对原分式方程进行化简然后代入即可;
②先对原分式方程进行化简然后代入即可.
②观察可得最简公分母是(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)①先对原分式方程进行化简然后代入即可;
②先对原分式方程进行化简然后代入即可.
解答:解:①方程两边都乘x(x+1),
得:2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
∴x=2是原方程的解;
②方程的两边同乘(x-3),得
2-x=x-3+1,
解得x=2.
检验:把x=2代入(x-3)≠0.
∴x=2是原方程的解,
(2)①原式=
=
,
将x=5,代入得:
=5,
②原式=(
-
)÷(
-
)=
,
将a=2,b=1代入得:
=3.
得:2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
∴x=2是原方程的解;
②方程的两边同乘(x-3),得
2-x=x-3+1,
解得x=2.
检验:把x=2代入(x-3)≠0.
∴x=2是原方程的解,
(2)①原式=
| x(x-4) |
| (x-4)2 |
| x |
| x-4 |
将x=5,代入得:
| 5 |
| 5-4 |
②原式=(
| a2- ab |
| (a-b)2 |
| a2 |
| (a-b)2 |
| a2- ab |
| a2-b2 |
| a2 |
| a2-b2 |
| a+b |
| a-b |
将a=2,b=1代入得:
| 2+1 |
| 2-1 |
点评:本题主要考查了解分式方程的一般步骤:(1)解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解,(2)解分式方程一定注意要代入最简公分母验根,(3)分式方程里单独的一个数和字母也必须乘最简公分母,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
 =1
=1 ,其中x=5.
,其中x=5. ,其中a=2,b=1.
,其中a=2,b=1. 的过程中,小王和小李的化简结果不一样:
的过程中,小王和小李的化简结果不一样: =
= =
= .
. =
=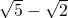 .
. ,求
,求
 的值.(结果保留根号)
的值.(结果保留根号)