题目内容
 如图所示,在数轴上点A所表示的数x的范围是
如图所示,在数轴上点A所表示的数x的范围是
- A.
 sin30°<x<sin60°
sin30°<x<sin60° - B.cos30°<x<
 cos45°
cos45° - C.
 tan30°<x<tan45°
tan30°<x<tan45° - D.
 cot45°<x<cot30°
cot45°<x<cot30°
D
分析:先根据数轴上A点的位置确定出其范围,再根据特殊角的三角函数值对四个选项进行分析即可.
解答:由数轴上A点的位置可知, <A<2.
<A<2.
A、由 sin30°<x<sin60°可知,
sin30°<x<sin60°可知, ×
× <x<
<x< ,即
,即 <x<
<x< ,故本选项错误;
,故本选项错误;
B、由cos30°<x< cos45°可知,
cos45°可知, <x<
<x< ×
× ,即
,即 <x<
<x<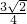 ,故本选项错误;
,故本选项错误;
C、由 tan30°<x<tan45°可知,
tan30°<x<tan45°可知, ×
× <x<1,即
<x<1,即 <x<1,故本选项错误;
<x<1,故本选项错误;
D、由 cot45°<x<cot30°可知,
cot45°<x<cot30°可知, ×1<x<
×1<x< ,即
,即 <x<
<x< ,故本选项正确.
,故本选项正确.
故选D.
点评:本题考查的是特殊角的三角函数值及在数轴的特点,熟记各特殊角的三角函数值是解答此题的关键.
分析:先根据数轴上A点的位置确定出其范围,再根据特殊角的三角函数值对四个选项进行分析即可.
解答:由数轴上A点的位置可知,
 <A<2.
<A<2.A、由
 sin30°<x<sin60°可知,
sin30°<x<sin60°可知, ×
× <x<
<x< ,即
,即 <x<
<x< ,故本选项错误;
,故本选项错误;B、由cos30°<x<
 cos45°可知,
cos45°可知, <x<
<x< ×
× ,即
,即 <x<
<x<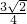 ,故本选项错误;
,故本选项错误;C、由
 tan30°<x<tan45°可知,
tan30°<x<tan45°可知, ×
× <x<1,即
<x<1,即 <x<1,故本选项错误;
<x<1,故本选项错误;D、由
 cot45°<x<cot30°可知,
cot45°<x<cot30°可知, ×1<x<
×1<x< ,即
,即 <x<
<x< ,故本选项正确.
,故本选项正确.故选D.
点评:本题考查的是特殊角的三角函数值及在数轴的特点,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )A、
| ||
B、cos30°<x<
| ||
C、
| ||
D、
|
 如图所示,在数轴上点A和B之间表示整数的点有( )
如图所示,在数轴上点A和B之间表示整数的点有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( ) 如图所示,在数轴上点A所表示的数为a,则a的值为( )
如图所示,在数轴上点A所表示的数为a,则a的值为( ) 如图所示,在数轴上点A表示的数可能是( )
如图所示,在数轴上点A表示的数可能是( )