题目内容
 如图,点A(2,4),B(4,2),若Q是x轴上使得QA十QB的值最小的点,则点Q的坐标为
如图,点A(2,4),B(4,2),若Q是x轴上使得QA十QB的值最小的点,则点Q的坐标为考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:找到B关于x轴对称点C,连接AC交x轴于Q点,易求得点C坐标,即可求得直线AC解析式,根据点Q为直线AC与x轴交点,即可求得点Q坐标,即可解题.
解答:解:找到B关于x轴对称点C,连接AC交x轴于Q点,

∵点B,C关于x轴对称,B(4,2),
∴点C坐标为(4,-2),
设直线AC解析式为y=kx+b,
代入A,C点得:
,
解得:k=-3,b=10,
∴直线AC解析式为y=-3x+10,
∵直线AC交x轴于Q点,
∴点Q纵坐标为0,
∵点Q横坐标x满足-3x+10=0,
解得:x=
,
∴点Q坐标为(
,0).
故答案为 (
,0).

∵点B,C关于x轴对称,B(4,2),
∴点C坐标为(4,-2),
设直线AC解析式为y=kx+b,
代入A,C点得:
|
解得:k=-3,b=10,
∴直线AC解析式为y=-3x+10,
∵直线AC交x轴于Q点,
∴点Q纵坐标为0,
∵点Q横坐标x满足-3x+10=0,
解得:x=
| 10 |
| 3 |
∴点Q坐标为(
| 10 |
| 3 |
故答案为 (
| 10 |
| 3 |
点评:本题考查了最短路线问题,考查了直线解析式的求解,考查了直线与坐标轴交点的求解,本题中求得直线AC的解析式是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
下列说法中,正确的是( )
| A、两点之间,线段最短 |
| B、射线OA与射线AO是同一条射线 |
| C、若线段AB=BC,则B是线段AC的中点 |
| D、连结两点的线段叫做这两点间的距离 |
 如图所示,一个水平放置的长方形水槽长18dm,宽12dm,高9dm,水深4dm,一个棱长为6dm的立方体铁块,以底面平行于液面的方式逐步没入水中,设铁块没入水中的高度为xdm,同时水面上升的相应高度为ydm,写出y关于x的函数表达式
如图所示,一个水平放置的长方形水槽长18dm,宽12dm,高9dm,水深4dm,一个棱长为6dm的立方体铁块,以底面平行于液面的方式逐步没入水中,设铁块没入水中的高度为xdm,同时水面上升的相应高度为ydm,写出y关于x的函数表达式 在△ABC中,AB=AC,BD平分∠ABC交AC于点D,若BD=BC,且AB=20,求BC的长.
在△ABC中,AB=AC,BD平分∠ABC交AC于点D,若BD=BC,且AB=20,求BC的长.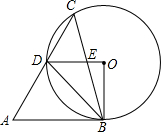 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论: