题目内容
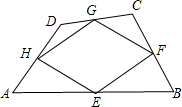如图，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四边形ABCD的值是________．
1：2
分析：连接AC，BD．由E，F，G，H是四边形ABCD各边的中点可求得三角形相似，从而求得两四边形的面积比．
解答：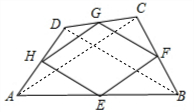
解：连接AC，BD．
因为G、F为CD、BC边中点，所以GF=
DB．
由于△CGF∽△CDB，所以
S△CGF=
S△CDB，
同理可得S△DHG=S△CDA，S△HAE=S△DAB，S△BEF=S△CAB，于是
S△CGF+S△DHG+S△HAE+S△BEF=（S△CDB+S△CDA+S△DAB+S△CAB）=×2S四边形ABCD=S四边形ABCD，
S四边形EFGH：S四边形ABCD=1：2
点评：本题考查了三角形中位线的性质及相似多边形的性质．相似多边形对应边之比、周长之比等于相似比，
分析：连接AC，BD．由E，F，G，H是四边形ABCD各边的中点可求得三角形相似，从而求得两四边形的面积比．
解答：
解：连接AC，BD．因为G、F为CD、BC边中点，所以GF=
DB．由于△CGF∽△CDB，所以
S△CGF=
S△CDB，同理可得S△DHG=
S△CDA，S△HAE=S△DAB，S△BEF=S△CAB，于是S△CGF+S△DHG+S△HAE+S△BEF=
（S△CDB+S△CDA+S△DAB+S△CAB）=×2S四边形ABCD=S四边形ABCD，S四边形EFGH：S四边形ABCD=1：2
点评：本题考查了三角形中位线的性质及相似多边形的性质．相似多边形对应边之比、周长之比等于相似比，
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
=2，∠ADC=30°
30、如图，已知直线a，b与直线c相交，下列条件中不能判定直线a与直线b平行的是（ ）
如图，已知：DE∥BC，AB=14，AC=18，AE=10，则AD的长为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
13、如图，已知直线AB∥CD，∠1=50°，则∠2=