题目内容
 如图、A、B、C、三市在同一直线上,某天然气公司的主输气管道从A市沿A→B→C→D的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西60°方向.C市在A市北偏东75°方向.B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据:
如图、A、B、C、三市在同一直线上,某天然气公司的主输气管道从A市沿A→B→C→D的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西60°方向.C市在A市北偏东75°方向.B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据: ,
, )
)
【答案】分析:由已知D地在A地北偏东45°方向,C地在A地北偏东75°方向,D地在A地北偏东45°方向可知∠DAB=30°∠ADB=45°,则在△ABD中已知两角和边BD=20km,求AD的长,可以通过作AD边上的高转化为解直角三角形解决.
解答: 解:过B作BH⊥AD于H.
解:过B作BH⊥AD于H.
依题意∠BDH=45°,∠CBD=75°,∠BAD=75°-45°=30°.
在Rt△BDH中,HD=BH=BD•cos45°=10 km,
km,
在Rt△ABH中,AH= =10
=10 ,
,
AB= =20
=20 ,
,
∴AD=AH+HD=10 +10
+10 ,
,
∵∠ABD=180°-75°=105°,
∴∠ADC=45°+60°=105°,
∴∠ABD=∠ADC.
又∵∠DAB=∠CAD,
∴△ABD∽△ADC,
∴ ,
,
即: ,
,
解得:AC=20 +10
+10 ,CD=10
,CD=10 +10.
+10.
故天然气从A市输送到D市的路程是AC+CD=20 +10
+10 +10
+10 +10≈79(km),
+10≈79(km),
答:天然气从A市输送到D市的路程约为79km.
点评:本题主要考查了方向角含义和相似三角形的判定以及性质,解题的关键是正确作出高线,利用特殊角的三角函数求出AD和AB的长.
解答:
 解:过B作BH⊥AD于H.
解:过B作BH⊥AD于H.依题意∠BDH=45°,∠CBD=75°,∠BAD=75°-45°=30°.
在Rt△BDH中,HD=BH=BD•cos45°=10
 km,
km,在Rt△ABH中,AH=
 =10
=10 ,
,AB=
 =20
=20 ,
,∴AD=AH+HD=10
 +10
+10 ,
,∵∠ABD=180°-75°=105°,
∴∠ADC=45°+60°=105°,
∴∠ABD=∠ADC.
又∵∠DAB=∠CAD,
∴△ABD∽△ADC,
∴
 ,
,即:
 ,
,解得:AC=20
 +10
+10 ,CD=10
,CD=10 +10.
+10.故天然气从A市输送到D市的路程是AC+CD=20
 +10
+10 +10
+10 +10≈79(km),
+10≈79(km),答:天然气从A市输送到D市的路程约为79km.
点评:本题主要考查了方向角含义和相似三角形的判定以及性质,解题的关键是正确作出高线,利用特殊角的三角函数求出AD和AB的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
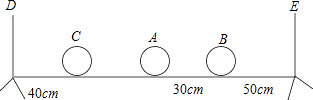
 19、如图,l1、l2、l3是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.
19、如图,l1、l2、l3是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处. 如图所示,两人准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?
如图所示,两人准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁? 如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1).
如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1).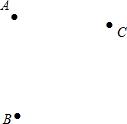 如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明)
如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明)