题目内容
 如图,在边长是20m的正方形池塘周围是草地,池塘边A,B,C,D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛拴在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子拴在
如图,在边长是20m的正方形池塘周围是草地,池塘边A,B,C,D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛拴在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子拴在
- A.A处或C处
- B.B处
- C.B处或D处
- D.D处
B
分析:根据圆的面积公式,以及扇形的面积公式,即可求得拴在各点时的活动区域的面积,即可作出判断.
解答:将牛栓在A上时,活动区域的面积是: π×22+
π×22+ π(
π( )2=2π+
)2=2π+ =
= π;
π;
将牛栓在B上时,活动区域的面积是: =
=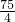 π;
π;
将牛栓在C上时,活动区域的面积是: π;
π;
将牛栓在D上时,活动区域的面积是: π×52=
π×52= π.
π.
则应栓在B处.
故选:B.
点评:此题主要考查了圆的面积公式以及扇形的面积公式,利用图形分别得出牛的活动范围是解题关键.
分析:根据圆的面积公式,以及扇形的面积公式,即可求得拴在各点时的活动区域的面积,即可作出判断.
解答:将牛栓在A上时,活动区域的面积是:
 π×22+
π×22+ π(
π( )2=2π+
)2=2π+ =
= π;
π;将牛栓在B上时,活动区域的面积是:
 =
=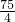 π;
π;将牛栓在C上时,活动区域的面积是:
 π;
π;将牛栓在D上时,活动区域的面积是:
 π×52=
π×52= π.
π.则应栓在B处.
故选:B.
点评:此题主要考查了圆的面积公式以及扇形的面积公式,利用图形分别得出牛的活动范围是解题关键.

练习册系列答案
相关题目
 如图,直角边长是20m的等腰直角三角形池塘周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛栓在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子栓在
如图,直角边长是20m的等腰直角三角形池塘周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛栓在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子栓在 如图,在边长是20m的正方形池塘周围是草地,池塘边A,B,C,D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛拴在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子拴在( )
如图,在边长是20m的正方形池塘周围是草地,池塘边A,B,C,D处各有一棵树,且AB=BC=CD=4m,现用长5m的绳子将一头牛拴在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子拴在( )
