题目内容
如图，直角边长是20m的等腰直角三角形池塘周围是草地，池塘边A、B、C、D处各有一棵树，且AB=BC=CD=4m，现用长5m的绳子将一头牛栓在一棵树上，为了使牛在草地上活动区域的面积最大，应将绳子栓在分析：根据圆的面积公式，以及扇形的面积公式，即可求得拴在各点时的活动区域的面积，即可作出判断．
解答：解：将牛栓在A上时，活动区域的面积是：
π×22+
π（
）2=2π+
=
π；
将牛栓在B上时，活动区域的面积是：
=
π；
将牛栓在C上时，活动区域的面积是：
π；
将牛栓在D上时，活动区域的面积是：
π×52=
π．
则应栓在B处．
故答案是：B．
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9π |
| 8 |
| 25 |
| 8 |
将牛栓在B上时，活动区域的面积是：
| 270π×52 |
| 360 |
| 75 |
| 4 |
将牛栓在C上时，活动区域的面积是：
| 25 |
| 8 |
将牛栓在D上时，活动区域的面积是：
| 1 |
| 2 |
| 25 |
| 2 |
则应栓在B处．
故答案是：B．
点评：本题主要考查了圆的面积公式以及扇形的面积公式，是基本的运算．
练习册系列答案
阅读快车系列答案
相关题目
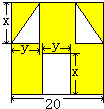“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．
（1）“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．