题目内容
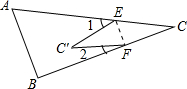 如图,将△ABC折叠,使点C落在点C′处,折痕为EF.
如图,将△ABC折叠,使点C落在点C′处,折痕为EF.(1)若∠1=40°,∠2=20°,求∠C;
(2)探究∠1,∠2与∠C之间的数量关系.
分析:(1)根据平角求出∠CEC′和∠CFC′,再根据翻折的性质求出∠CEF和∠CFE,然后利用三角形的内角和定理列式进行计算即可得解;
(2)用∠1、∠2表示出∠CEC′和∠CFC′,再根据翻折的性质表示出∠CEF和∠CFE,然后根据三角形的内角和定理列式整理即可得解.
(2)用∠1、∠2表示出∠CEC′和∠CFC′,再根据翻折的性质表示出∠CEF和∠CFE,然后根据三角形的内角和定理列式整理即可得解.
解答:解:(1)∵∠1=40°,∠2=20°,
∴∠CEC′=180°-∠1=180°-40°=140°,
∠CFC′=180°-∠2=180°-20°=160°,
由翻折的性质,∠CEF=
∠CEC′=
×140°=70°,
∠CFE=
∠CFC′=
×160°=80°,
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-70°-80°=30°;
(2)∠CEC′=180°-∠1,∠CFC′=180°-∠2,
由由翻折的性质,∠CEF=
∠CEC′,∠CFE=
∠CFC′,
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-
(180°-∠1)-
(180°-∠2),
=180°-90°+
∠1-90°+
∠2,
=
(∠1+∠2),
所以,∠1+∠2=2∠C.
∴∠CEC′=180°-∠1=180°-40°=140°,
∠CFC′=180°-∠2=180°-20°=160°,
由翻折的性质,∠CEF=
| 1 |
| 2 |
| 1 |
| 2 |
∠CFE=
| 1 |
| 2 |
| 1 |
| 2 |
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-70°-80°=30°;
(2)∠CEC′=180°-∠1,∠CFC′=180°-∠2,
由由翻折的性质,∠CEF=
| 1 |
| 2 |
| 1 |
| 2 |
在△CEF中,∠C=180°-∠CEF-∠CFE=180°-
| 1 |
| 2 |
| 1 |
| 2 |
=180°-90°+
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
所以,∠1+∠2=2∠C.
点评:本题考查了三角形的内角和定理,翻折的性质,利用平角和翻折前后两个角相等表示出∠CEF和∠CFE是解题的关键.

练习册系列答案
相关题目
 18、如图,将△ABC的∠C折叠,使C点在AC边上,折痕为DE,则( )
18、如图,将△ABC的∠C折叠,使C点在AC边上,折痕为DE,则( )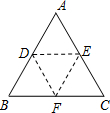 如图,将△ABC沿DE折叠,使点A与BC的中点F重合,下列结论:①EF∥AB,且EF=
如图,将△ABC沿DE折叠,使点A与BC的中点F重合,下列结论:①EF∥AB,且EF=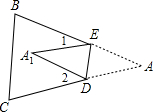
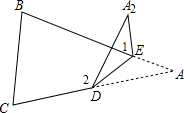
 如图,将△ABC折叠,使点C落在点C′处,折痕为EF.
如图,将△ABC折叠,使点C落在点C′处,折痕为EF.