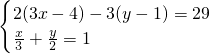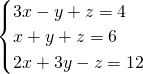Question

解方程租：
（1）

2(3x-4)-3(y-1)=29 x 3 + y 2 =1

（ 2）

3x-y+z=4 x+y+z=6 2x+3y-z=12

Answer 1

分析：（1）先将两方程分别通过去括号，去分母，化为最简形式，再用消元法，①+②消去y，解得x的值，再求出y的值．
（2）本题采用消元法解，①-②，②+③，消去Z，化为二元一次方程组，再采用消元法，即可解得方程组的解．

解答：解：（1）

2(3x-4)-3(y-1)=29 x 3 + y 2 =1

化简得

6x-3y=34 2x+3y=6

，
①+②，得x=5，再代入任一个方程中，
解得

x=5 y=- 4 3

；

（2）①-②，②+③，得

x-y=-1 3x+4y=18

，
再用消元法①×4+②，得x=2，y=3，
再代入x+y+z=6中，解得z=1，
∴

x=2 y=3 z=1

．

点评：本题的实质是考查三元一次方程组的解法．需要对三元一次方程组的定义有一个深刻的理解．方程组有三个未知数，每个方程的未知项的次数都是1，并且一共有三个方程，像这样的方程组，叫三元一次方程组．通过解方程组，了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法，从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法．解三元一次方程组的关键是消元．解题之前先观察方程组中的方程的系数特点，认准易消的未知数，消去未知数，组成元该未知数的二元一次方程组．