Question

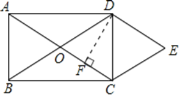
【题目】如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．

(1)求证：四边形OCED是菱形．

(2)当∠ACB=30°，菱形OCED的面积为，求AC的长．

Answer 1

【答案】（1）证明见解析；（2）AC=4．

【解析】

（1）首先由CE∥BD，DE∥AC，可证得四边形CODE是平行四边形，又由四边形ABCD是矩形，根据矩形的性质，易得OC=OD，即可判定四边形OCED是菱形．

（2）因为∠ACB=30°可证明菱形的一条对角线和边长相等，可证明和对角线构成等边三角形，然后作辅助线，根据菱形的面积已知可求解．

（1）解：∵CE∥BD，DE∥AC，

∴四边形CODE是平行四边形，

∵四边形ABCD是矩形，

∴AC=BD，OA=OC，OB=OD，

∴OD=OC，

∴四边形OCED是菱形；

（2）解：∵∠ACB=30°，

∴∠DCO=90°-30°=60°．

又∵OD=OC，

∴△OCD是等边三角形．

过D作DF⊥OC于F，则CF=OC，设CF=x，则OC=2x，AC=4x．

在Rt△DFC中，tan60°=，

∴DF=x．

∴OCDF=2．

∴x=1．

∴AC=1×4=4．