��Ŀ����
����Ŀ���Ķ����в��ϲ��ش����⣮����֪����![]() ��
��![]() ����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����
����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����![]() ��
��![]() ��Ϊ��������ʽ��
��Ϊ��������ʽ��![]() ��
��![]() ��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺
��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺![]() �������������⣺
�������������⣺
��1��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��
��2�����㣺![]() ��
��
��3����ʵ��![]() ��
��![]() ���ж�
���ж�![]() ��
��![]() �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�
���𰸡���1��![]() ��
�� ![]() ����2��3����3��
����2��3����3��![]() �����ɼ�����
�����ɼ�����
��������
��1��ֱ��������������ʽ�ĸ�������ó��𰸣�
��2��������������ʽ�ĸ��������𰸣�
��3��ֱ��������������ʽ�ĸ��������𰸣�
�⣺��1��![]() ��
��![]() ��
��
��2��![]()
![]()
![]() ��
��
��3��![]() ��
��
�������£�
���㣺![]() ��
��![]() ��
��
![]() ��
��
![]() ����
����![]() ��
��

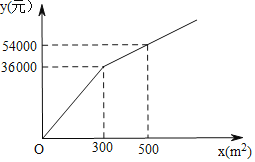
����Ŀ����֪һˮ�ص��ݻ�V����������ע��ˮ��ʱ��t�����ӣ�֮�俪ʼ��һ�κ�����ϵ�����м�¼�������ʱ��ע��ˮ��ʱ����ˮ���ݻ����ֶ�Ӧֵ��
ע��ˮ��ʱ��t�����ӣ� | 0 | 10 | �� | 25 |
ˮ�ص��ݻ�V�������� | 100 | 300 | �� | 600 |
��1�������ʱ��ʱV����t�ĺ�����ϵʽ������Ҫд�������Ķ�����
��2����tΪ25���ӿ�ʼ��ÿ����ע���ˮ�������仯�ˣ���tΪ27����ʱ��ˮ�ص��ݻ�Ϊ726������������������е�ÿ����ע���ˮ�������İٷ�����ͬ��������ٷ��ʣ�