题目内容
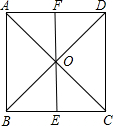 如图所示,正方形ABCD的边长为2,AC和BD相交于点O,过O作EF∥AB,交BC于E,交AD于F,则以点B为圆心,
如图所示,正方形ABCD的边长为2,AC和BD相交于点O,过O作EF∥AB,交BC于E,交AD于F,则以点B为圆心,| 2 |
分析:此题重点是根据题意和正方形的性质,分别找到圆心到直线的距离,再根据数量关系判断其位置关系.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答:解:由题中已知条件,得
BO⊥AC,BO=
BD=
=
,
即点B到AC的距离为
,与⊙B的半径相等;
∴直线AC与⊙B相切.
∵EF∥AB,∠ABC=90°,
∴BE⊥EF,垂足为E.
且BE=
BC=
×2=1<
,
∴直线EF与⊙B相交.
BO⊥AC,BO=
| 1 |
| 2 |
| 1 |
| 2 |
| BC2+CD2 |
| 2 |
即点B到AC的距离为
| 2 |
∴直线AC与⊙B相切.
∵EF∥AB,∠ABC=90°,
∴BE⊥EF,垂足为E.
且BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴直线EF与⊙B相交.
点评:考查了直线和圆的位置关系与数量之间的关系.此题一定要正确找到圆心到直线的距离.

练习册系列答案
相关题目
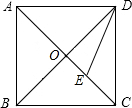 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
 4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )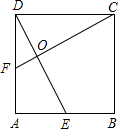 如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF.
如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF. 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: