题目内容
己知二次函数y=-x2+x+2图象与坐标轴交于三点A,B,C,则经过这三点的外接圆半径为________.

分析:设抛物线y=-x2+x+2与y轴的交点为A,与x轴的交点分别为B、C两点,先求出A、B、C三点的坐标,设经过这三个点的外接圆的圆心为M(m,n),由AM=BM=CM即可求出m、n的值,进而得出外接圆的半径.
解答:设抛物线y=-x2+x+2与y轴的交点为A,与x轴的交点分别为B、C两点,
令x=0,则y=2,
则点A的坐标为:(0,2),
令y=0,则-x2+x+2=0,解得x=2或x=-1,
故B(2,0),C(-1,0),
设经过这三个点的外接圆的圆心为M(m,n),
则
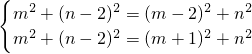 ,
,解得:
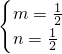 ,
,故点M坐标为(
 ,
, ),
),故外接圆的半径AM=
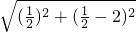 =
= .
.故答案为:
 .
.点评:本题考查抛物线与坐标轴的交点、三角形的外接圆,根据题意得出A、B、C三点的坐标是解答此题的关键,要求同学们掌握三角形外接圆圆心到三角形各顶点的距离相等.

练习册系列答案
相关题目
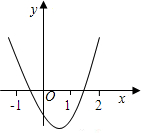 己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)a-b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第四象限.其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
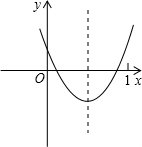 己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (2013•燕山区一模)己知二次函数
(2013•燕山区一模)己知二次函数 (2013•松北区三模)如图,己知二次函数y=-
(2013•松北区三模)如图,己知二次函数y=-