题目内容
16.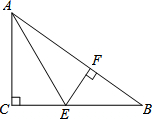 如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.
如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.
分析 根据角的平分线的性质可求得CE=EF,然后根据直角三角形的判定定理求得三角形全等,得到AC=AF,由于点F是AB的一个三等分点,设BF=m,则AC=2m,AF=2m,AB=3m,根据勾股定理得到BF=$\sqrt{5}$,AB=3$\sqrt{5}$,通过△BEF∽△ABC,即可得到结论.
解答 解:∵AE是∠BAC的平分线,EC⊥AC,EF⊥AF,
∴CE=EF,
在Rt△ACE与Rt△AFE中,
$\left\{\begin{array}{l}{CE=EF}\\{AE=AE}\end{array}\right.$,
∴Rt△ACE≌Rt△AFE(HL),
∴AC=AF,
∵点F是AB的一个三等分点,
设BF=m,则AC=2m,AF=2m,AB=3m,
∴AB2=BC2+AC2,
∴(3m)2=52+(2m)2,
∴m=$\sqrt{5}$,
∴BF=$\sqrt{5}$,AB=3$\sqrt{5}$
∵∠BFE=∠C=90°,∠B=∠B,
∴△BEF∽△ABC,
∴$\frac{BE}{AB}=\frac{BF}{BC}$,即$\frac{BE}{3\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴BE=3.
点评 本题考查了角平分线的性质,解直角三角形,全等三角形的判定和性质,相似三角形的判定和性质,根据已知条件表示出线段的值是解本题的关键.

练习册系列答案
相关题目
 小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面五条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0;⑤b+2c>0.你认为正确信息的个数有( )
小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面五条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0;⑤b+2c>0.你认为正确信息的个数有( ) 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.
如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF. 经过两个已知点A、B能确定一个圆吗?经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
经过两个已知点A、B能确定一个圆吗?经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?