题目内容
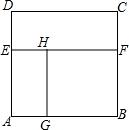 如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么
如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么| b | a |
分析:先用a、b、c分别表示出长方形CDEF与AGHE的面积,再根据题意得a-b=c,将c消掉,从而得出
的值即可;然后再表示出正方形BFHG与正方形ABCD的面积,通过a=3b得出正方形BFHG与正方形ABCD的面积比.
| b |
| a |
解答:解:∵长方形CDEF与AGHE的面积分别为ab和c(a-c),
∴ab:c(a-c)=3:2,
又∵c=a-b,∴
=
,
整理得3b2=ab,
∴
=
,
∴a=3b,
∵正方形BFHG与正方形ABCD的面积分别为(a-b)2和a2,
∴
=
=
=
,
故答案为
;
.
∴ab:c(a-c)=3:2,
又∵c=a-b,∴
| ab |
| b(a-b) |
| 3 |
| 2 |
整理得3b2=ab,
∴
| b |
| a |
| 1 |
| 3 |
∴a=3b,
∵正方形BFHG与正方形ABCD的面积分别为(a-b)2和a2,
∴
| (a-b)2 |
| a2 |
| (3b-b)2 |
| (3b)2 |
| 4b2 |
| 9b2 |
| 4 |
| 9 |
故答案为
| 1 |
| 3 |
| 4 |
| 9 |
点评:本题考查了面积及等积变换,利用a、b、c分别表示出长方形CDEF与AGHE的面积,正方形BFHG与正方形ABCD的面积是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
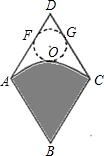 如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.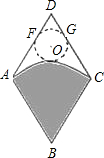 如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.
如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形. 如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
如图,从一个边长为1米的正方形铁皮中剪下一个扇形. );
);