题目内容
倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径。下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题。
习题解答:
习题 如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由。
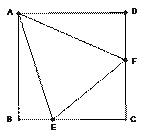
习题研究
 观察分析 观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;
观察分析 观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;
④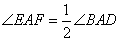 。答:成立。
。答:成立。
类比猜想
(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,
∠B=∠D,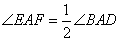 时,还有EF=BE+DF吗?答:不一定成立。
时,还有EF=BE+DF吗?答:不一定成立。
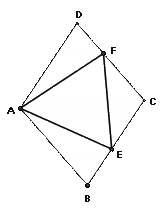
研究一个问题,常从特例入手,请同学们研究:如图(2),在菱
形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°
时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,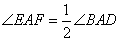 时,EF=BE+DF吗?
时,EF=BE+DF吗?
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把⊿ABE绕点A逆时针旋转90°至⊿ADE/ ,点F、D、E/在一条直线上。
,点F、D、E/在一条直线上。
∴∠E/AF=90°-45°=45°=∠EAF,
又∵AE/=AE,AF=AF
∴⊿AE/F≌⊿AEF(SAS)
∴EF=E/F=DE/+DF=BE+DF。
答:BE+DF EF.
EF.
答:成立。
归纳概括 反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题:
在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,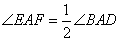 时,总有EF=BE+DF 成立。
时,总有EF=BE+DF 成立。

下面的多项式在实数范围内能因式分解的是( )
|
| A. | x2+y2 | B. | x2﹣y | C. | x2+x+1 | D. | x2﹣2x+1 |
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )

|
| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
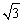 km C.2
km C.2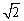 km D.(
km D.(

 了解学生每
了解学生每
 8 28 C25 28 D28 31
8 28 C25 28 D28 31