题目内容
如图，在△ABC中，∠ACB=120°，CD平分∠ACB，AE∥DC，交BC的延长线于点E，试说明△ACE是等边三角形．
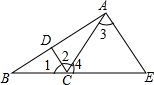
证明：∵CD平分∠ACB，∠ACB=120°
∴∠1=∠2=
=
=60°
∵AE∥DC
∴∠3=∠2=60°，∠E=∠1=60°
∴∠3=∠4=∠E=60°
∴△ACE是等边三角形．
∴∠1=∠2=
| ∠ACB |
| 2 |
| 120° |
| 2 |
∵AE∥DC
∴∠3=∠2=60°，∠E=∠1=60°
∴∠3=∠4=∠E=60°
∴△ACE是等边三角形．
练习册系列答案
相关题目
Q，连CP．
