题目内容
18．
如图，在某公路上有A、B两点，两点间的距离为20千米，在距A点正北方8千米处有一个村庄D，在距B点正南方12千米处有一个村庄C，现在要在公路旁边修建一个停车点，使得停车点到C、D两村的距离相等，请你算一算，停车点应距A点多少千米？
分析 根据题意得出DE=EC，再利用勾股定理得出答案．
解答 
解：如图所示：由题意可得，DE=EC，
AD=8km，BC=12km，BE=20-AE，
则AD2+AE2=BE2+BC2，
即82+AE2=（20-AE）2+122，
解得：AE=12，
答：停车点应距A点12千米．
点评 此题主要考查了勾股定理的应用，得出DE=EC进而结合勾股定理求出是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
6．
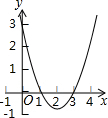二次函数y=x2-4x+3的图象如图所示，利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是（ ）
二次函数y=x2-4x+3的图象如图所示，利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是（ ）| A． | 0＜x＜1 | B． | 1＜x＜2 | C． | 2＜x＜3 | D． | x＞3 |
10．关于x的方程ax2-3x+（a-2）=0是一元二次方程，则（ ）
| A． | a＞0 | B． | a≠0 | C． | a=0 | D． | a≥0 |