题目内容
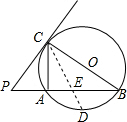
如图，在△ABC中，AC=6，BC=8，AB=10，以AC为直径作⊙O交AB于点D．
（1）判断直线BC和⊙O的位置关系，并说明理由；
（2）求AD的长．
（1）判断直线BC和⊙O的位置关系，并说明理由；
（2）求AD的长．
（1）∵AC=6，BC=8，AB=10，
∴AB2=AC2+BC2，∴∠ACB=90°，（2分）
又∵AC是⊙O的直径，
∴直线BC和⊙O相切．（4分）
（2）由（1）得BC2=BD•BA，
∴82=BD×10，
∴BD=
，（6分）
∴AD=AB-BD=10-
=
．（8分）．
∴AB2=AC2+BC2，∴∠ACB=90°，（2分）
又∵AC是⊙O的直径，
∴直线BC和⊙O相切．（4分）
（2）由（1）得BC2=BD•BA，
∴82=BD×10，
∴BD=
| 32 |
| 5 |
∴AD=AB-BD=10-
| 32 |
| 5 |
| 18 |
| 5 |
练习册系列答案
相关题目
点F，E为垂足．
