题目内容
2. 如图,已知AD∥BC,AB∥DC,DE⊥AB,DF⊥BC,垂足分别是E,F,并且DE=DF.求证:
如图,已知AD∥BC,AB∥DC,DE⊥AB,DF⊥BC,垂足分别是E,F,并且DE=DF.求证:(1)∠A=∠C;
(2)四边形ABCD是菱形.
分析 (1)根据平行四边形的性质得出∠A=∠C;
(2)根据菱形的判定得出即可.
解答  证明:(1)证法(一)∵AD∥BC,AB∥DC,
证明:(1)证法(一)∵AD∥BC,AB∥DC,
∴ABCD是平行四边形,
∴∠A=∠C;
证法(二)∵AD∥BC,
∴∠A+∠B=180°,
∵AB∥DC,
∴∠B+∠C=180°,
∴∠A=∠C;
(2)在△AED和△CFD中,
$\left\{\begin{array}{l}{∠AED=∠CFD}\\{∠A=∠C}\\{DE=DF}\end{array}\right.$,
∴△AED≌△CFD(AAS),
∴AD=CD.
∵ABCD是平行四边形,
∴ABCD是菱形.
点评 此题主要考查了菱形的性质和全等三角形的判定等知识,根据已知得出∠A=∠C是解题关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
12.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查我市中学生每天体育锻炼的时间 | |
| B. | 调查某班学生的视力情况 | |
| C. | 调查一架“歼20”隐形战机各零部件的质量 | |
| D. | 调查伦敦奥运会女子铅球参赛运动员兴奋剂的使用情况 |
7.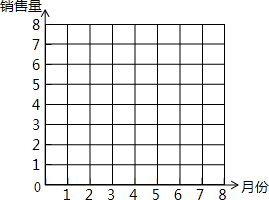 甲、乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:
甲、乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:
(1)在图给出的图形中,绘制甲、乙两人这8个月的销售量的折线图;(甲用实线,乙用虚线)
(2)请根据(1)中的折线统计图,写出2条关于甲、乙两人在这8个月中的销售状况的信息.
 甲、乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:
甲、乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:| 月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
| 甲的销售量(单位:台) | 7 | 8 | 6 | 7 | 6 | 6 | 7 | 7 |
| 乙的销售量(单位:台) | 5 | 6 | 5 | 6 | 7 | 7 | 8 | 9 |
(2)请根据(1)中的折线统计图,写出2条关于甲、乙两人在这8个月中的销售状况的信息.