题目内容
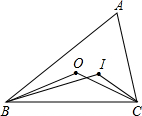如图，点O和点I分别是△ABC的外心和内心，若∠BOC=130°，则∠BIC=________．
122.5°
分析：利用三角形外心的性质以及圆周角定理得出∠A的度数，进而利用内心的知识得出∠IBC+∠ICB的度数，即可得出答案．
解答：∵点O是△ABC的外心，∠BOC=130°，
∴∠A=65°，
∴∠ABC+∠ACB=115°，
∵点I是△ABC的内心，
∴∠IBC+∠ICB=
×115°=57.5°，
∴∠BIC=180°-57.5°=122.5°．
故答案为：122.5°．
点评：此题主要考查了三角形内心和外心的综合应用，根据题意得出∠IBC+∠ICB的度数是解题关键．
分析：利用三角形外心的性质以及圆周角定理得出∠A的度数，进而利用内心的知识得出∠IBC+∠ICB的度数，即可得出答案．
解答：∵点O是△ABC的外心，∠BOC=130°，
∴∠A=65°，
∴∠ABC+∠ACB=115°，
∵点I是△ABC的内心，
∴∠IBC+∠ICB=
×115°=57.5°，∴∠BIC=180°-57.5°=122.5°．
故答案为：122.5°．
点评：此题主要考查了三角形内心和外心的综合应用，根据题意得出∠IBC+∠ICB的度数是解题关键．
练习册系列答案
相关题目
如图，点A和点B分别在双曲线y=
