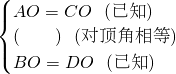题目内容
已知∠AOB与∠COD互余(∠COD的两边不在∠AOB的内部),OM平分∠AOC,ON平分∠BOD,将∠COD绕着点O逆时针旋转,使∠BOC=α(0°≤α<180°).
(1)若∠AOB=60°,∠COD=30°.
①当α=0°时,即OB与OC重合时,如图1,则∠MON=
②当α=90°时,即OA与OD在一条直线上,如图2,求∠MON的度数.
③当α=140°时,请补全图形(如图3),并求出∠MON的度数.
(2)若∠AOB=β,∠COD=γ(β>γ),则∠MON=
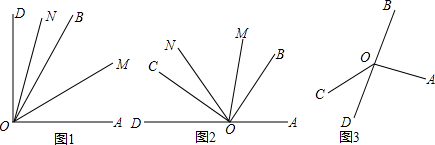
(1)若∠AOB=60°,∠COD=30°.
①当α=0°时,即OB与OC重合时,如图1,则∠MON=
45°
45°
.②当α=90°时,即OA与OD在一条直线上,如图2,求∠MON的度数.
③当α=140°时,请补全图形(如图3),并求出∠MON的度数.
(2)若∠AOB=β,∠COD=γ(β>γ),则∠MON=
45°或135°
45°或135°
.
分析:(1)先根据角平分线的定义得出∠MOB=
∠AOB,∠BON=
∠BOD,再根据∠MON=∠MOB+∠BON即可求解;
(2)由特殊到一般可求∠MON的度数即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由特殊到一般可求∠MON的度数即可.
解答:解:(1)①∠MON=
∠AOC+
∠BOD=45°.
②当α=90°时,
∠MON=180°-(
∠AOC+
∠BOD)
=180°-[
(∠AOB+∠BOC)+
(∠COD+∠BOC)]
=180°-[
(60°+90°)+
(30°+90°)]
=45°.
③当α=140°时,
∵∠AOD=360°-60°-30°-140°=130°,
∴∠MON=
∠AOC+
∠BOD-∠COD
=
(∠AOD+∠DOC)+
(∠BOC+∠COD)-∠COD
=
(∠AOD+∠BOC)
=
(360°-90°)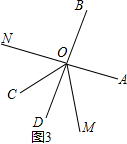
=135°;
(2)当∠AOB=β,∠COD=γ(β>γ)时,∠AOB与∠COD互余,则β+γ=90°,
当如图1所示:∠MON=
∠AOC+
∠BOD=
(β+γ)=45°,
如图3所示:
∠MON=
∠AOC+
∠BOD-∠COD
=
(∠AOD+∠DOC)+
(∠BOC+∠COD)-∠COD
=
(∠AOD+∠BOC)
=
(360°-∠AOB-∠COD)
=
(360°-90°)
=135°,
则∠MON=135°或45°.
故答案为:135°或45°.
| 1 |
| 2 |
| 1 |
| 2 |
②当α=90°时,
∠MON=180°-(
| 1 |
| 2 |
| 1 |
| 2 |
=180°-[
| 1 |
| 2 |
| 1 |
| 2 |
=180°-[
| 1 |
| 2 |
| 1 |
| 2 |
=45°.
③当α=140°时,
∵∠AOD=360°-60°-30°-140°=130°,
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |

=135°;
(2)当∠AOB=β,∠COD=γ(β>γ)时,∠AOB与∠COD互余,则β+γ=90°,
当如图1所示:∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图3所示:
∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=135°,
则∠MON=135°或45°.
故答案为:135°或45°.
点评:本题主要考查了学生在学习过程中对角度关系及运算的灵活运用和掌握.此类题目的练习有利于学生更好的对角的理解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
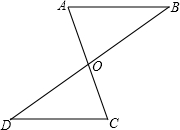 .
. 25、如图,在?ABCD中,AC与BD相交于点O,∠AOD=∠CBO,
25、如图,在?ABCD中,AC与BD相交于点O,∠AOD=∠CBO,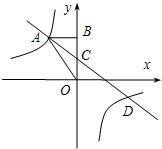 如图,已知一次函数y1=kx+b(k≠0)与反比例函数
如图,已知一次函数y1=kx+b(k≠0)与反比例函数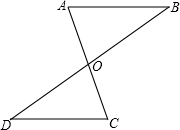 .
.