题目内容
 如图所示,OE为∠COA的平分线,∠AOE=β,∠AOB=∠COD=α.
如图所示,OE为∠COA的平分线,∠AOE=β,∠AOB=∠COD=α.(1)用α、β表示∠BOC;
(2)比较∠AOC与∠BOD的大小.
分析:(1)由OE为角平分线,得到∠COA=2∠AOE,再由∠BOC=∠COA-∠AOB表示即可;
(2)根据∠BOD=∠BOC+∠COD,表示出∠BOD,即可确定出∠AOC与∠BOD的大小.
(2)根据∠BOD=∠BOC+∠COD,表示出∠BOD,即可确定出∠AOC与∠BOD的大小.
解答:解:(1)∵OE为∠COA的平分线,
∴∠COA=2∠AOE=2β,
∴∠BOC=∠COA-∠AOB=2β-α;
(2)∵∠BOD=∠BOC+∠COD=2β-α+α=2β,
∴∠AOC=∠BOD.
∴∠COA=2∠AOE=2β,
∴∠BOC=∠COA-∠AOB=2β-α;
(2)∵∠BOD=∠BOC+∠COD=2β-α+α=2β,
∴∠AOC=∠BOD.
点评:此题考查了角的计算,以及角平分线定义,熟练掌握角平分线定义是解本题的关键.

练习册系列答案
相关题目
 如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
 18、如图所示,E为平行四边形ABCD边CD延长线上的一点,连接BE交AC于O,交AD于F,请说明BO2=OF•OE.
18、如图所示,E为平行四边形ABCD边CD延长线上的一点,连接BE交AC于O,交AD于F,请说明BO2=OF•OE.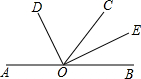 如图所示,O为直线AB上一点,过O点作射线OC.已知OD平分∠AOC、OE平分∠BOC,请问OD与OE有什么位置关系?并说明理由.
如图所示,O为直线AB上一点,过O点作射线OC.已知OD平分∠AOC、OE平分∠BOC,请问OD与OE有什么位置关系?并说明理由. 如图所示,OE为∠COA的平分线,∠AOE=β,∠AOB=∠COD=α.
如图所示,OE为∠COA的平分线,∠AOE=β,∠AOB=∠COD=α.