题目内容
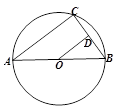
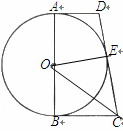
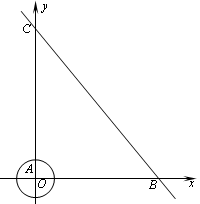
如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB。

(1)求证:BC为⊙O的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G。若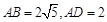 ,求线段BC和EG的长。
,求线段BC和EG的长。

(1)求证:BC为⊙O的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G。若
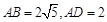 ,求线段BC和EG的长。
,求线段BC和EG的长。(1)连接OE,OC,先根据“SSS”证得△OBC≌△OEC,即可得到∠OBC=∠OEC,再根据切线的性质可得∠OEC=90,即可得到∠OBC=90,从而证得结果;(2)BC=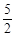 ,
,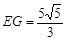
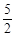 ,
,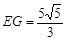
试题分析:(1)连接OE,OC,先根据“SSS”证得△OBC≌△OEC,即可得到∠OBC=∠OEC,再根据切线的性质可得∠OEC=90,即可得到∠OBC=90,从而证得结果;
(2)过点D作DF⊥BC于点F,根据切线的性质可得DA=DE,CE=CB,设BC为
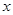 ,则CF=x-2,DC=x+2,在Rt△DFC中,根据勾股定理即可列方程求得x的值,根据平行线的性质可得∠DAE=∠EGC,由DA=DE可得∠DAE=∠AED,再结合∠AED=∠CEG即可求得CG=CE=CB=
,则CF=x-2,DC=x+2,在Rt△DFC中,根据勾股定理即可列方程求得x的值,根据平行线的性质可得∠DAE=∠EGC,由DA=DE可得∠DAE=∠AED,再结合∠AED=∠CEG即可求得CG=CE=CB=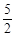 ,再根据勾股定理求得AG的长,然后证得△ADE∽△GCE,根据相似三角形的性质即可求得结果.
,再根据勾股定理求得AG的长,然后证得△ADE∽△GCE,根据相似三角形的性质即可求得结果.(1)连接OE,OC,
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC,
∴∠OBC=∠OEC,
又∵与DE⊙O相切于点E,
∴∠OEC=90,
∴∠OBC=90,
∴BC为⊙
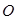 的切线;
的切线;(2)过点D作DF⊥BC于点F,
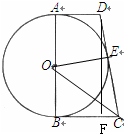
∵AD,DC,BG分别切⊙O于点A,E,B,
∴DA=DE,CE=CB,设BC为
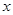 ,则CF=x-2,DC=x+2,
,则CF=x-2,DC=x+2,在Rt△DFC中,
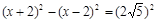 ,解得
,解得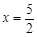 ,
,∵AD∥BG
∴∠DAE=∠EGC,
∵DA=DE
∴∠DAE=∠AED,
∵∠AED=∠CEG,
∴∠ECG=∠CEG。
∴CG=CE=CB=
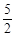
∴BG=5,
∴
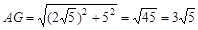
∵∠DAE="∠EGC" ,∠AED=∠CEG
∴△ADE∽△GCE,
∴
 ,
,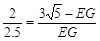 ,解得
,解得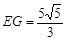 .
.点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,需仔细分析.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 .
.

 EF长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为( )
EF长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为( )
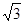 cm
cm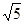 cm
cm