题目内容
 在△ABC中,D为AB的中点,分别延长CA、CB到点E、F,使DE=DF,过E、F分别作CA、CB的垂线相交于P,设线段PA、PB的中点分别为M、N.
在△ABC中,D为AB的中点,分别延长CA、CB到点E、F,使DE=DF,过E、F分别作CA、CB的垂线相交于P,设线段PA、PB的中点分别为M、N.求证:①△DEM≌△DFN;
②∠PAE=∠PBF.
分析:①要证△DEM≌△DFN,由D、M、N分别是AB、AP、BP的中点,所以DM=
BP,DN=
AP,再有过E、F分别作CA、CB的垂线相交于P,
所以EM=
AP=DN,FN=
BP=DM.又DE=DF所以△DEM≌△DFN.
②由①得∠EMD=∠FND,由∠AMD=∠BND=∠APB所以∠AME=∠BNF,那么∠PAE=
(180°-∠AME),∠PBF=
(180°-∠BNF),即∠PAE=∠PBF.
| 1 |
| 2 |
| 1 |
| 2 |
所以EM=
| 1 |
| 2 |
| 1 |
| 2 |
②由①得∠EMD=∠FND,由∠AMD=∠BND=∠APB所以∠AME=∠BNF,那么∠PAE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:①如图,在△ABP中,
∵D、M、N分别是AB、AP、BP的中点,
∴DM=
BP,DN=
AP,
又∵PE⊥AE,BF⊥PF
∴EM=
AP=DN,FN=
BP=DM,
∵DE=DF
∴△DEM≌△DFN(SSS);
②∵由①结论△DEM≌△DFN可知∠EMD=∠FND,
∵DM∥BP,DN∥AP,
∴∠AMD=∠BND=∠APB,
∴∠AME=∠BNF
又∵PE⊥AE,BF⊥PF,
∴△AEP和△BFP都为直角三角形,
又M,N分别为斜边PA与PB的中点,
∴AM=EM=
AP,BN=NF=
BP,
∴∠MAE=∠MEA,∠NBF=∠NFB,
∴∠PAE=
(180°-∠AME),∠PBF=
(180°-∠BNF).
即∠PAE=∠PBF,
∵D、M、N分别是AB、AP、BP的中点,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
又∵PE⊥AE,BF⊥PF
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE=DF
∴△DEM≌△DFN(SSS);
②∵由①结论△DEM≌△DFN可知∠EMD=∠FND,
∵DM∥BP,DN∥AP,
∴∠AMD=∠BND=∠APB,
∴∠AME=∠BNF
又∵PE⊥AE,BF⊥PF,
∴△AEP和△BFP都为直角三角形,
又M,N分别为斜边PA与PB的中点,
∴AM=EM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MAE=∠MEA,∠NBF=∠NFB,
∴∠PAE=
| 1 |
| 2 |
| 1 |
| 2 |
即∠PAE=∠PBF,
点评:此题考查了线段之间的关系,和全等三角形的判定和性质,同学们应该熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.
已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.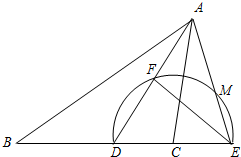 AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.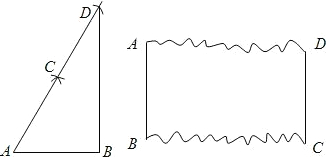
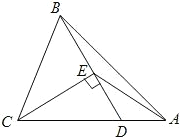
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.