题目内容
 如图,圆柱的底面直径为8cm,高为10cm.动点P从A点出发,沿圆柱的侧面移动到BC的中点S的最短距离是
如图,圆柱的底面直径为8cm,高为10cm.动点P从A点出发,沿圆柱的侧面移动到BC的中点S的最短距离是13
13
cm(π取3).分析:由于圆柱底面直径为8cm,高为10cm,S为BC的中点,故BS=5cm,先把圆柱的侧面展开,连接AS,利用勾股定理即可得出AS的长.
解答: 解:∵直径为8cm,高为10cm,S为BC的中点,
解:∵直径为8cm,高为10cm,S为BC的中点,
∴圆柱底面圆的半径是2cm,BS=5cm,
∴
=
×π×8=4π=12,
如图所示:连接AS,在Rt△ABS中,
AS=
=13.
故答案为13.
 解:∵直径为8cm,高为10cm,S为BC的中点,
解:∵直径为8cm,高为10cm,S为BC的中点,∴圆柱底面圆的半径是2cm,BS=5cm,
∴
 |
| AB |
| 1 |
| 2 |
如图所示:连接AS,在Rt△ABS中,
AS=
| 122+52 |
故答案为13.
点评:本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 cm,高为
cm,高为 cm. 动点
cm. 动点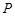 从
从 点出发,沿圆柱的侧面移动到
点出发,沿圆柱的侧面移动到 的中点
的中点 的最短距离是 cm(
的最短距离是 cm( 取
取 ).
).
 cm,高为
cm,高为 cm. 动点
cm. 动点 从
从 点出发,沿圆柱的侧面移动到
点出发,沿圆柱的侧面移动到 的中点
的中点 的最短距离是 cm(
的最短距离是 cm( 取
取 ).
).
 B.
B. C.
C. D.
D.





