题目内容
在平面直角坐标系中,点(2,-3)在第____象限.
四 【解析】∵点的横纵坐标均为负数,∴点(﹣2,﹣3)在第三象限.故答案为:三.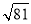 的平方根为_____.
的平方根为_____.
关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A. 点(0,k)在l上
B. l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大
D. l经过第一、二、三象限
查看答案如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
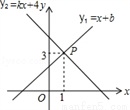
A. x>﹣2 B. x>0 C. x>1 D. x<1
查看答案在元旦联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为游戏公平,则凳子应放的最适当的位置是△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边上高的交点 D. 三边垂直平分线的交点
查看答案下列各组数不能作为直角三角形边长的是( )
A. 3,4,5 B. 8,15,17 C. 7,9,11 D. 9,12,15
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 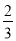 B.
B. 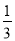 C.
C. 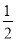 D.
D. 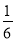
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )
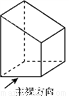

A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=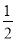 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;
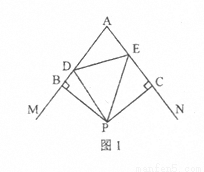
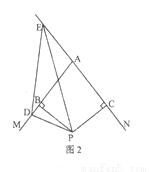
(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。
阅读下列材料:
(1)解方程: 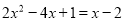
【解析】
方程化为: 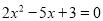 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=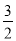 或x=1.
或x=1.
∴方程的根为: 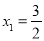 ,
, 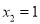 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 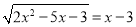 ;
;
(2)若方程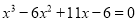 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算: 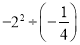 =_____.
=_____.
若|x+2|+|y﹣3|=0,则x﹣y的值为_____.
查看答案图中以点O为端点的射线有_____条,图中共有_____条线段.
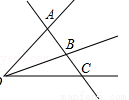
如图,把弯曲的河道改直,能够缩短航程,这样做根据的道理是_____.
如图所示,边长为a的正方形中阴影部分的面积为( )
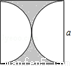
A. a2﹣π(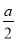 )2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
)2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
下列各组整式中不是同类项的是( )
A. 3a2b与﹣2ba2 B. 2xy与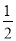 yx C. 16与﹣
yx C. 16与﹣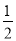 D. ﹣2xy2与3yx2
D. ﹣2xy2与3yx2
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
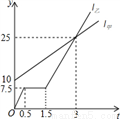
(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
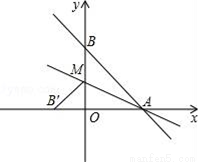
(1)10;(2)1;(3) 乙出发3小时时,在距乙出发点25km处,乙追上甲;(4) 在距乙的出发点15km处,乙追上甲. 【解析】(1)根据图象,当t=0时,两个函数的图象的纵坐标的差就是所求; (2)根据乙的图象即可直接求解; (3)根据横纵坐标的实际应用是关键; (4)利用待定系数法求得甲的函数解析式以及乙出发时y与t的函数解析式,然后解两个解析式组成的方程组即可求...如图,直线y=﹣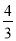 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.
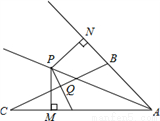
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB,PM⊥AC,垂足分别为点N,M.求证:BN=CM
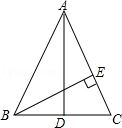
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算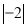 +(3-π)0-2-1+
+(3-π)0-2-1+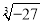
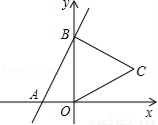
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
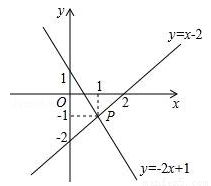
如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组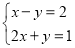 的解是 .
的解是 .
已知a、b、c是△ABC的三边长,且满足关系式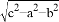 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
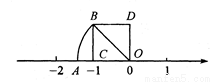
查看答案如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.
某人一天饮水1890mL,用四舍五入法对1890mL精确到1000mL表示为____mL.
查看答案在平面直角坐标系中,点(2,-3)在第____象限.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各组数不能作为直角三角形边长的是( )
A. 3,4,5 B. 8,15,17 C. 7,9,11 D. 9,12,15
C 【解析】A.∵ ,∴3,4,5可以作为直角三角形的边长; B.∵ ,∴8,15,17可以作为直角三角形的边长; C.∵ ,∴7,9,11可以作为直角三角形的边长; D.∵ ,∴9,12,15可以作为直角三角形的边长; 故选C.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
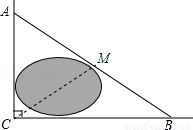
A. 0.5km B. 0.6km C. 0.9km D. 1.2km
查看答案如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
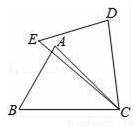
A. BC=EC,∠B=∠E B. BC=EC,AC=DC C. BC=DC,∠A=∠D D. ∠B=∠E,∠A=∠D
查看答案下列各数中,3.141 59, 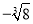 ,0.131 131 113…,-π,
,0.131 131 113…,-π, 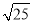 ,
, 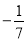 ,无理数的个数有( )
,无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案在下列“禁毒”“和平”“志愿者”“节水”这四个标志中,属于轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
从2012年4月1日起厦门市实行新的自来水收费阶梯水价,收费标准如下表所示:
月用水量 | 不超过15吨的部分 | 超过15吨不超过25吨的部分 | 超过25吨的部分 |
收费标准 (元/吨) | 2.2 | 3.3 | 4.4 |
备注:①.每月居民用水缴费包括实际用水的水费和污水处理费两部分.
②.以上表中的价格均不包括1元/吨的污水处理费
(1)某用户12月份用水量为20吨,则该用户12月份应缴水费是多少?
(2)若某用户的月用水量为m吨,请用含m的式子表示该用户月所缴水费.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
定义:若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣x与 是关于1的平衡数.(用含x的代数式表示)
(2)若a=2x2﹣3(x2+x)+4,b=2x﹣[3x﹣(4x+x2)﹣2],判断a与b是否是关于1 的平衡数,并说明理由.
(1)﹣1;x﹣3;(2)a与b不是关于1的平衡数 【解析】试题分析:(1)由平衡数的定义即可求得答案; (2)计算a+b是否等于1即可. 试题解析:(1)设3的关于1的平衡数为a,则3+a=2,解得a=﹣1, ∴3与﹣1是关于1的平衡数, 设5﹣x的关于1的平衡数为b,则5﹣x+b=2,解得b=2﹣(5﹣x)=x﹣3, ∴5﹣x与x﹣3是关于1的平衡数, ...某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:千米)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣10,+6,﹣3,﹣6,﹣4,+10
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若出租车每千米的耗油量为0.08升,这天下午出租车共耗油量多少升?
查看答案在数轴上表示下列各数,并用“<”连接起来.
﹣4,﹣|﹣2.5|,﹣(﹣2),0,﹣12.
查看答案先化简,再求值:x2﹣3(2x2﹣4y)+2(x2﹣y)其中x=﹣2,y=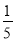 .
.
化简:
(1)﹣3xy﹣2y2+5xy﹣4y2
(2)2(5a2﹣2a)﹣4(﹣3a+2a2)
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知 a、b两数在数轴上对应的点如图所示,下列结论正确的是( )
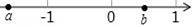
A. ab>0 B. |a|>|b| C. a﹣b>0 D. a+b>0
B 【解析】依题意得:a<﹣1,1>b>0, ∴a、b异号,且|a|>|b|, ∴a+b<0,a﹣b=﹣|a+b|<0,ab<0, 故选B.某商品进价a元,商店将价格提高30%作零售价销售,在销售旺季过后,商店以8折的价格开展促销活动,这时一件商品的售价为( )
A. a元 B. 1.04a元 C. 0.8a元 D. 0.92a元
查看答案已知|x|=3,|y|=2,且x•y<0,则x+y的值等于( )
A. 5或﹣5 B. 1或﹣1 C. 5或1 D. ﹣5或﹣1
查看答案一个多项式加上多项式2x﹣1后得3x﹣2,则这个多项式为( )
A. x﹣1 B. x+1 C. x﹣3 D. x+3
查看答案下列式子中,不能成立的是( )
A. ﹣(﹣2)=2 B. ﹣|﹣2|=﹣2 C. 23=6 D. (﹣2)2=4
查看答案若有理数a的值在﹣1与0之间,则a的值可以是( )
A. ﹣2 B. 1 C. 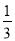 D.
D. 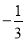
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
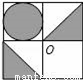
A.  B.
B.  C.
C. 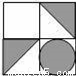 D.
D. 
下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B. 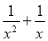 =2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
【解析】
∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值;
(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.
查看答案某商家预测一种衬衫能畅销市场,就用12000元购进了一批这种衬衫,上市后果然供不应求,商家又用了26400元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但每件进价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫都按每件150元的价格销售,则两批衬衫全部售完后的利润是多少元?
查看答案若x=2m+1,y=3+4m.
(1)请用含x的代数式表示y;
(2)如果x=4,求此时y的值.
查看答案解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=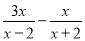 ,B=
,B=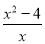 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧